6.3 Identische Teilchen

N Teilchen sind identisch, wenn keine dynamische Eigenschaft des System sich ändert unter beliebigen Permutationen. Zum Zeitpunkt t = 0 haben wir einen Zustand |₀> und zum Zeitpunkt t haben wir U(t,t₀)|₀>. Lassen wir eine Permutation auf den Zustand wirken, so gilt zum Zeitnullpunkt P|t₀> und zum Zeitpunkt t finden wir U(t,t₀)P|₀>. Man kann auch zuerst die zeitliche Entwicklung des Systems anwenden un danach die Permutation, also PU(t,t₀)|₀>. Es gilt U(t,t₀)P|₀> = PU(t,t₀)|₀>, weil es sich um „identische“ Teilchen handelt. Damit kommutieren die beiden Operatoren, also [P,U] = 0.

Erinnern wir uns an folgende Differentialgleichung für U(t,t₀):

Deren Lösung ist:

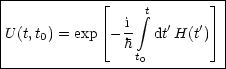
Damit finden wir, daß für identische Teilchen P und H vertauschen, also [P,H] = 0.

Betrachten wir nun eine Observable A des Systems.

Zustand	|>
Messung (ergibt Resultat a)	A|> = a|>	AP|> = aP|>
		PA|> = aP|>

Auch hieraus ergibt sich dann, daß P und A vertauschen, daß also [P,A] = 0 gilt.

Betrachten wir nochmals die symmetrischen und antisymmetrischen Vektoren:

• P|u> = |u>
• P|v> = (-)^p|v>

Wir wollen zeigen, daß die symmetrischen Vektoren senkrecht zu den antisymmetrischen sind. P ist unitär, es gilt also P^-1 = P^†. Mit PP = 1 folgt P = P^†, womit P auch hermitesch ist. Aus P|u> = |u> und P|v> = -|v> ergibt sich <u|v> = 0, womit die Vektoren senkrecht aufeinander stehen.