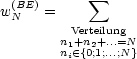6.6 Fermionen und Fermi-Dirac-Statistik

Es seien N Teilchen im Unterraum E_N^(A) E in der Q-Darstellung gegeben.

A |qn11,qn22,...> /= 0

Nehmen wir an, daß es einen Besetzungsgrad J_k gibt mit n_k > 2.

( ) Ji,j|qn11,qn22,...> = |...,q(ki),...,q(kj)...> = 1+-P(ij)- |...,q(ik),...,q(jk)...> 2

Lemma:

P(j) A(1 + Pij) = A+ (- ) A = A - A = 0

Dies führt zum sogenannten Paulischen Ausschließungsprinzip. Dieses besagt, daß zwei Fermionen nicht denselben Einzelteilchenzustand besetzen können. Wir nehmen nun einen bestimmten Vektor |q⁽¹⁾,q⁽²⁾,...,q^(N)> und führen folgende Operation durch:

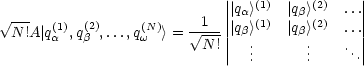
|||qa>(1) |qb>(2) ...|| V~ --- (1) (2) (N) -1--|||q>(1) |q >(2) ...|| N!A|qa ,qb ,...,qw > = V~ N-!|| b. b. . || | .. .. ..|

Für N = 1 ist die Beziehung trivial. Für N = 2 gilt für die linke Seite der Gleichung:

V~ - ( ) |y> = 2.1-. |q(1a),q(b2)>- |q(a2)q(b1)> 2

Für die rechte Seite der Gleichung erhalten wir die Slater-Determinante:

| | -1-|||qa>(1) |qa>(2)|| 1--( (1) (2) (2) (1)) V~ 2-||qb>(1) |qb>(2)|= V~ 2 |qa ,qb >- |qa qb >

Damit haben wir die Gleichung für den Fall N = 2 gezeigt. Betrachten wir nun die verschiedenen Statistiken:

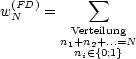
Fermi-Dirac-Statistik: $w(FD)= sum N Verteilung n1+n2+...=N ni (- {0;1}$
Dieses findet Anwendung bei:
- Helium-Atom (Ortho- und Parahelium)
- Stoß zweier identischer Teilchen
Bose-Einstein-Statistik: $(BE) sum wN = nV1e+rnte2il+u..n.=gN ni (- {0;1;...;N}$

[prev] [prev-tail] [front] [up]