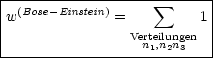6.5 Bosonen und Bose-Einstein-Statistik

N Teilchen befinden sich im Zustandsraum E_N^(S) E in der Q-Darstellung. In jedem Unterraum E_{n₁,n₂,n₃,...} mit n₁ + n₂ + ... = N E_N^(S) suchen wir genau einen symmetrischen und normierten Vektor:

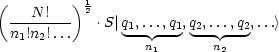
( )1 ---N!--- 2 .S|q1,...,q1,q2,...,q2,...> n1!n2!... --- --- --- --- n1 n2

Die n₁ ersten Teilchen besetzen den Zustand |q₁> usw. Damit haben wir unseren Hilbertraum eingeschränkt.

6.5.1 Bosonengas

Es handelt sich um eine große Anzahl ohne Wechselwirkung in der Q-Darstellung:

H = h(1) + h(2) + ...+ h(N)

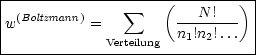
BOLTZMANN besagt nun, daß sich ein System in einem thermodynamischen Gleichgewicht ist, wenn sich dieses in seinem wahrscheinlichsten „makroskopischen“ Zustand befindet. Es gibt sehr viele Mikrozustände, welche einen Makrozustand beschreiben. Die Wahrscheinlichkeit ist proportional zur Anzahl der Mikrozustände, welche natürlich kompatibel mit dem Makrosystem sind. Ein Mikrozustand, bei welchem sich beispielsweise alle Luftmoleküle im Hörsaal auf einer Seite befinden, beschreibt das Makrosystem nicht.

Jede Verteilung {n₁,n₂,n₃,...|n₁ + n₂ + ... = N} der N Bosonen auf die verschiedenen Einzelzustände |q₁>, |q₂>, ... definiert genau einen Mikrozustand.

|-------------------------| w(Bose-Einstein) = sum 1| | Verteilungen | ------------------n1,n2n3----

|-------------------------------| | (Boltzmann) sum ( N ! ) | |w = n-!n-!... | -------------Verteilung--1--2------

[next] [prev] [prev-tail] [front] [up]