7.7 Zeitumkehroperator

Betrachten wir zuerst ein Teilchen ohne Spin. Wir wollen den betreffenden Operator als K bezeichnen mit den Eigenschaften KK^† = und K K^† = - . Beispielsweise vertauschen x und p_x nicht: [x,p_x] = i. Durch Anwendung des Operators K folgt K[x,p_x]K^† = KiK^†. Andererseits muß gelten K[x,-p_x]K^† = -K[x,p_x]K^† = -KiK^†. K muß somit i in -i überführen. K muß damit „antiunitär“ sein:

KihK † = (-ih)KK † = - ih

K(r × p)K † = -(r× p) ==> KJK † = - J

K ändert sowohl den Impulsoperator als auch Drehimpulsoperatoren. In der Wellenmechanik bezeichnen wir den Komplexkonjugations-Operator mit K₀; es gilt also durch Anwendung von K₀ auf einen Zustand (): K₀() = ^*() und außerdem [K₀,H] = 0.

K0ih @-|y(t)> = K0H |y(t)> @t

Aufgrund der Vertauschungsrelation von K₀ mit H ergibt sich:

-@ - ih@tK0 |y(t)> = HK0 |y(t)>

Schreiben wir nun t = -t':

@ ih--'K0|y(-t')> = HK0 |y(- t')> @t

Lassen wir nun einfach den Strich weg:

|----------------------------| @- | @- | ih@tK0|y(-t)> = HK0 |y(-t)> <==> ih@t [K0|y(-t)>] =-H-[K0-|y(--t)>]

Wir haben damit eine neue Lösung der Gleichung gefunden, nämlich |(t)>_umk K₀|(-t)>. Betrachten wir nun ein Teilchen mit Spin: Hier gilt dann K = - K und außerdem lieht Antiunitarität vor. Schauen wir, was mit dem Drehoperator R nach einer Zeitumkehr passiert:

[ i ] [ i ] [ i ] K exp -h-J^uf K † = exp +h-KJ ^uK †f = exp - hJ ^uf

Damit gilt also KR = RK und somit [K,R] = 0; die Operatoren R und K vertauschen also. Angenommen, wir haben nun ein Teilchen mit dem Spin s in der {,S_z}-Darstellung:

K0rK † = r, K0pK †= - p 0 0

Außerdem gilt:

{ Sx } { Sx } K0 Sy K †0 = - Sy Sz Sz

Für S = gilt:

{ ( ) ( ) ( )} S = 1s = 1 0 1 , 0 i , 1 0 2 2 1 0 - i 0 0 -1

Da die zweite Paulimatrix imaginär ist, entsteht das Minuszeichen! Dies gilt auch in der Standarddarstellung:

1 1 Jx = -(J+ + J- ) und Jy =-(J+- J- ) 2 2i

Wir wollen aber, daß dies für alle Operatoren s_x, s_y und s_z gilt. Machen wir deshalb den Ansatz K = RK₀, wobei R unitär und K antiunitär ist. R muß folgende Eigenschaften haben:

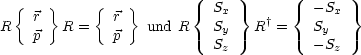
{ } { } { Sx } { -Sx } R r R = r und R Sy R † = Sy p p Sz -Sz

Diese Eigenschaften sind gerade dann erfüllt, wenn R eine Drehung im die y-Achse beschreibt:

|--------------------------| | [ S ] | R = R(S^ypin)(p) =_ exp - ip-y- | -----------------------h----

Für N Teilchen mit Gesamtspin S gilt:

|--------[-----]----| | Sy- | |K = exp -ip h K0 | --------------------

Wir schreiben nun N = N_halb + N_ganz. Wenden wir den Zeitumkehroperator K zweimal an, so folgt K² = (-1)^N_halb.

[ ipSy] [ ihSy] [ 2piSy] [ 2piSy] K2 = exp ---h- K0exp ---h- K0 = exp - -h--- K20 = exp - --h-- .1

Für solche Drehungen um 2 gilt (wie wir zuvor gesehen haben):

[ ] exp - 2piSy = (1)Ngang(- 1)Nhalb h

Eine Folgerung daraus ist die sogenannte KRAMERS-Entartung. Sei der nun Hamiltonoperator „reell“, also gilt KHK^† = H (1). Nehmen wir an, daß wir einen Eigenvektor |u> haben mit H|u> = E|u> (2). Des weiteren ist H hermitesch, womit E reell ist (3). Dann ist die Behauptung, daß auch K|u> Eigenvektor von H ist. Wir wollen dies beweisen. Dazu wenden wir H auf K|u> an:

H (K|u>) = KH |u>=1KH |u > 2= KE |u> 3= E (K|u>)

7.7.1 KRAMERS-Entartung

Haben wir eine ungerade Anzahl von 1/2-Spins, dann gibt es eine orthonormierte Basis mit Paaren von komplex konjugierten Vektoren. Dann liegt eine 2n-fache Entartung vor (KRAMERS-Entartung, 1930).

Beweis:

Betrachten wir zuerst den Fall K² = 1. Dann ist die Behauptung, daß |u> und K|u>proportional sind. Wir wenden K auf |u> an:

2 K |u> = exp (ia)K |u> ==> K |u> = exp(-ia)K | u> = exp(-ia)| u >

Daraus ergibt sich dann exp(i)K|u> = |u>. Für K² = -1 behaupten wir, daß |u> und K|u> unabhängig sind. Dies zeigen wir analog:

K |u> = exp(ia)K|u> ==> K |u> = exp(- ia)(-1)|u> ==> |u> = - exp(ia)K |u >

Dies ist nur erfüllt für |u> = 0, womit also |u> = exp(i)K|u> falsch sein muß!

[prev] [prev-tail] [front] [up]