7.6 Zeitumkehr

• Klassisch:

  Betrachten wir als erstes das Problem klassisch. Wir schauen uns ein Teilchen in einem statischen Potential an. Dann gilt für die Hamilton-Funktion:

  

  Für jede Lösung (t) kann ich eine andere Lösung _umk(t) (-t) und _umk = - _umk finden.

  

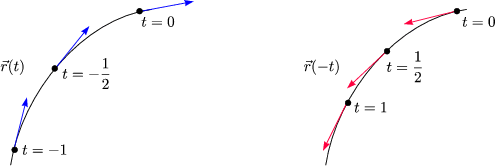
  Man durchläuft die Bahn also mit entgegengesetzter Geschwindigkeit. Mathematisch kann man zwar t durch -t ersetzen, aber physikalisch läuft die Zeit immer weiter. Hier ist jedoch Vorsicht geboten. Für ein klassisches System mit Magnetfeld gilt:

  

  

• Quantenmechanisch:

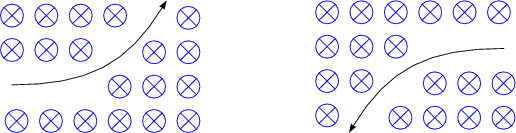
  Kommen wir nun zur Quantenmechanik. Hier gilt die Schrödingergleichung:

  

  Ersetzt man nun t durch -t, so erhalten wir auf den linken Seite aufgrund der zeitlichen Ableitung ein Minuszeichen. Wir führen also eine „Zeitumkehr“ und eine komplexe Konjugation durch:

  

  Wir definieren also:

  

  Sei eine Lösung, so ist _umk auch eine Lösung der Schrödingergleichung. Da dies für ein Problem mit einem Magnetfeld klassisch schon nicht geklappt hat, wird dies auch quantenmechanisch fehlschlagen.