7.5 Erhaltungssätze und Zeittranslation

Wir betrachten die Gruppe der Translationen GT_i G T_i.

Es liegt hier Invarianz einer Observablen O vor. Dies bedeutet für alle T_i G, daß [T_i,O] = 0 ist. Eine irreduzible Darstellung besitzt Basisvektoren |,j,>, wo zur Unterscheidung der Basisvektoren innerhalb einer Darstellung gilt. j kennzeichnet, um welche Darstellung es sich handelt und sind zusätzliche Quantenzahlen. Man kann nun ableiten, daß für die Matrixelemente gilt: <,j,|O|',j','> = _jj''O_'^(j). Damit sind alle Matrixelemente gleich 0 bis auf die Diagonalelemente (vergleiche Wigner-Eckart-Theorem für skalare Operatoren). Ebenso ist der Hamilton-Operator symmetrisch; es gilt also für alle T_i, daß [T_i,H] = 0.

Betrachten wir die Heisenberg-Gleichung für die Observable A mit = 0:

Jede Observable, die Funktion der Operatoren der Symmetriegruppe ist, ist eine Konstante der Bewegung _____________________.

Wenn Symmetrien also vorausgesetzt sind, finden wir Erhaltungssätze. Diese sind sehr wichtig für das Verständnis der Natur. Betrachten wir dazu folgende Beispiele:

• Drehinvarianz:

  Hier vertauscht der Hamilton-Operator mit dem Generator der Drehungen, also dem Drehimpuls. Es gilt also [H, ] = 0 und damit ist = const. im Heisenberg-Bild.

• Translationsinvarianz:

  In diesem Falle vertauscht H mit dem Generator , womit der Gesamtimpuls erhalten ist: = 0.

• Zeittranslationsinvarianz:

  Der Generator für Zeittranslationen ist gerade der Hamilton-Operator und der vertauscht mit sich selbst, so daß gilt [H,H] = 0. Daraus folgt Energieerhaltung.

• Spiegelungsinvarianz:

  Hier kommutiert H mit P und daraus ergibt sich Paritätserhaltung.

  

• Phaseninvarianz:

  Wir nennen den entsprechenden Generator Q und dann gilt [H,Q] = 0, womit Q also konstant ist. Diese Invarianz hat etwas mit Ladungserhaltung (Weyl) zu tun.

Später werden wie die Punkte 2a.) und 2b.) in der speziellen Relativitätstheorie zusammenfassen, wenn wir Vierer-Vektoren einführen.

Auch der Schrödinger-Entwicklungsoperator U kann invariant sein. (Dieser besitzt nämlich eine Integraldarstellung mit H und vertauscht deswegen auch mit H.) Für alle T_i muß daher [T_i,U(t,t₀)] = 0 gelten. Die Bewegungsgleichungen sind dann invariant, es sind also folgende Erwartungswerte für alle T_k gleich:

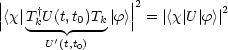
Damit gilt nach Satz 1:

Meistens ist _k = 0 und damit vertauschen die T_k und H: [T_k,H] = 0.