8.1 Definition

Wir wählen die Einheiten = 1 und c = 1. Die elektrischen Ladungen sind dann dimensionslose Größen:

Damit ist die Feinstrukturkonstante ce² . Pauli hat diese Konstante nie verstanden; er ist schließlich in einem Krankenhaus auf Zimmer 137 gestorben.

Dies gilt für einen Impulsübertrag von p² = mc². Wir benutzen außerdem die Gaußschen Einheiten (cgs-System) (siehe Jackson). Die Koordinaten eines Raum-Zeit-Punktes werden wir schreiben als (x⁰,x¹,x²,x³), also x (x0,x^m) = (x⁰,x¹,x²,x³) = (ct,x²,x2,x3). Betrachten wir nun den Minkowski-Tensor. Dabei handelt es sich um einen pseudo-euklidischen Tensor:

Wir unterscheiden außerdem zwischen:

• Kovariante Vektoren V

  Ein Beispiel hierfür ist .

• Kovarianter Vektor: K

  Ein Beispiel ist dx.

Mittels des Minkowski-Tensors können kontravariante und kovariante Vektoren ineinander umgewandelt werden:

Wenn ein Index oben und unten gleich ist, wird über diese Indizes nach der Einsteinschen Summenkonvention summiert. Es gilt also:

Mit diesen Vektoren läßt sich nun ein Skalarprodukt zweier Vierervektoren A und B bilden:

Klassifizierung:

8.1.1 Differentialoperator

• Gradientenoperator:

• d’Alembert-Operator:

8.1.2 Elektromagnetisches Feld

Es handelt sich um ein Vierer-Vektor-Feld. Damit können wir den elektromagnetischen Feld-Tensor definieren:

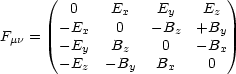
Aus der Elektrodynamik kennen wir außerdem folgenden Beziehungen:

Der Differentialoperator muß eich-kovariant sein:

Eichinvarianz bedeutet für beliebige Funktion g(x) :

Dies klappt nur, wenn A'(x) einen Verschiebungsterm enthält: A'(x) = A(x)-g(x) ist. Wenn sich das Potential mit einer Ableitung ändert, gilt F' = F.

F' = F ist also eichinvariant und D''(x) = exp(ix))D ist eichkovariant.