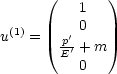8.10 Ebene Wellen

[next] [prev] [prev-tail] [tail] [up]

8.10 Ebene Wellen

Wir betrachten A(x) = 0 (DIRAC-Darstellung). Wichtig ist, daß H_D mit kommutiert, also [H_D, ] = 0. Wir bestimmen die Eigenlösungen von H_D zu einem bestimmen Wert . Wie können wir die Wellenfunktion aufschreiben?

y(x) = u(p)exp(ipr)

Wir haben (x) also separiert in einen konstanten Spinor u( ) und eine ebene Welle exp(i ). u( ) muß eine Lösung folgender Eigenwertgleichung sein:

HDu(p) =_ [a.p +bm] u(p) = Eu(p)

Die Spinoren sind Eigenlösungen zum Hamiltonoperator H_D.

( ) H2 = |p |2 + m2 1

Daraus ergeben sich dann die Energieeigenwerte E = ± ±E( ). Im Ruhesystem gilt p = (m,0,0,0). Betrachten wir mu(0) = Eu(0):

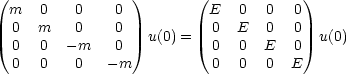
( ) ( ) m 0 0 0 E 0 0 0 0 m 0 0 u(0) = 0 E 0 0 u(0) 0 0 -m 0 0 0 E 0 0 0 0 -m 0 0 0 E

Hieraus lassen sich direkt die Eigenwerte E = ±m ablesen. Für die Eigenvektoren gilt:

(1) (0 ) (0) (0 ) (0) 0 (0) 1 (0) 0 (0) 0 u(1) = 0 , u(2) = 0 , u(3) = 1 , u(4) = 0 0 0 0 1

Daher gilt im Ruhesystem:

y(20)(x) = u(2)(0)exp(-iEt)

Betrachten wir nun einen Lorentz-Boost in z-Richtung: p' = (E',0,0,p'). Dann gilt in der DIRAC-Darstellung:

( ) ( ) ( ) y(2)(x') = /\u(2)(0)exp ip'mx'm mit /\ =_ cosh j-+is12sinh j-, s12 =_ i[g1,g2] 2 2 2

( 1 ) 0 u(1) = p' E'+ m 0

[next] [prev] [prev-tail] [front] [up]