9.1 Definition der Wirkungsquerschnitte

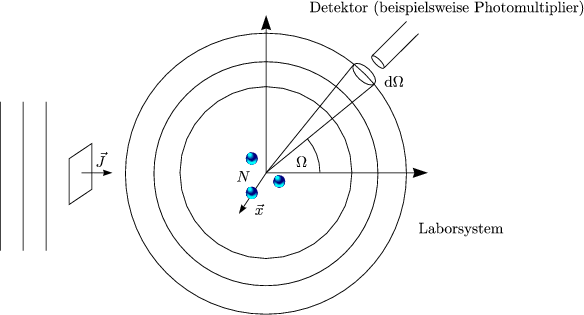
Betrachten wir folgendes Experiment:

Wir führen die Größe ein, welche maßgebend für die pro Zeiteinheit in den Raumwinkel d in die Richtung (,) gestreuten Teilchen ist. ist proportional zur Anzahl der Targets N, zum Betrag der Stromdichte J der gestreuten Teilchen und zum Raumwinkelelement d. Wir fassen dies zusammen als = () ^.J ^.N d, wobei wir () als differentiellen Streuquerschnitt bezeichnen. Schreiben wir die Einheitengleichung auf:

[ ] [ ] j = s(_O_)JN d_O_ 1 = [cm2]. --1--- .[1].[1] s cm2 .s

Die Gesamtzahl aller gestreuten Teilchen ergibt sich dann als:

integral jtot = J .N .stot mit stot = s(_O_)dw

Das Problem ist, den Streuquerschnitt zur berechnen. Dazu betrachten wir nun eine elastische Streuung von Teilchen der Masse m an einem statischen Potential V () mit lim_|x|||V () = 0. Diese Teilchen besitzen die Energie E und den Impuls = mit k ||. Für jeden Wert von gibt es eine Lösung der stationären Schrödingergleichung

[ ] - h2 /_\ +V (x) y (x) = Ey (x) 2m k k

deren Verhalten im Unendlichen von der Form ()exp(i) + f() (mit r = ||) ist. Damit haben wir zwei Wellen:

Welle der Dichte 1 mit der Stromdichte .
Die Dichte P ist definiert durch P = ()^*() und für die Stromdichte gilt:
$h [ ] @ J(x) =---- y* \~/ y - y\ ~/ y* mit--P + \~/ .J = 0 2mi @t$
Die Stromdichte kann auf diese Weise (als Übung) berechnet werden.
Welle der Dichte mit der Stromdichte x.
Auch dies kann mit den obigen Beziehungen für und P gezeigt werden.

Die Zahl der pro Zeiteinheit in den Raumwinkel (,d) emittierten Teilchen ist:

hk (f (_O_))2 2 -m- -r-- r d_O_

Diese Zahl dividiert durch den einfallenden Strom J = ergibt dann den Streuquerschnitt () = |f()|², wobei man f() als Streuamplitude bezeichnet.

9.1.1 Intermezzo

Betrachten wir die stationäre Schrödingergleichung:

[ 2 ] --h- /_\ + V (r) y(x) = Ey(x) 2m

V (r) soll ein Zentralpotential sein. Mit p_r r und = $(x× \~/ )$ erhalten wir daraus:

|[-----------------]--------------------| | -p2r -|l| 2-- | | 2m + 2mr2 + V(r) y(r,h,f) = Ey(r,h,f)| ----------------------------------------|

Hierbei gelten folgende Eigenwertgleichungen bei | |² und l_z:

| |²Y _l^m(,) = l(l + 1)²Y _l^m
l_zY _l^m = mY _l^m

Die Kugelfunktionen Y _l^m bilden auf der Einheitskugel ein vollständiges Orthonormalsystem von quadratintegrablen Funktionen. Zur Lösung der Schrödingergleichung führen wir eine Trennung der Variablen durch, also:

|------------------------| | m yl(r) m | y-l (r,h,f)-=--r-Yl-(h,f)-|

Durch Einsetzen erhalten wir folgende Gleichung, welche nur noch den Radialanteil y_l(r):

[ 2 2 2 ] --h--d- + h--l(l+-1) + V(r)- E yl(r) = 0 mit yl(0) = 0 2m dr2 2m r2

E < 0: Nur für diskrete Energiewerte gilt y_lexp(-kr) für r
E > 0: Bei beliebigen Energien gilt y_lsin mit der Phasenverschiebung _l

[next] [front] [up]