9.2 Streuphasen

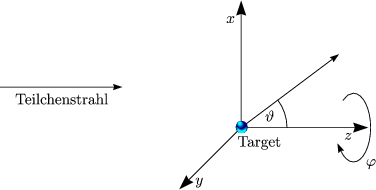
Betrachten wir also Teilchen im Zentralpotential V (r) mit lim_rrV = 0. Hierbei ist || .

Nun ist y_l die im Ursprung reguläre Lösung der Radialgleichung:

Hierbei findet man das asymptotische Verhalten y_la_l sin für r, wobei _l die Streuphase ist. Es gilt:

Daraus folgt die Streuamplitude mit und 1:

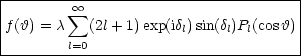
Wir vergleichen dies mit der Form von ebenen Wellen, wobei wir diese nach Legendre-Koeffizienten entwickeln:

Der Unterschied steckt in der Phase exp(2i_l) der auslaufenden Kugelwelle oder mit anderen Worten: Die Wirkung des Streupotentials besteht in einer Phasenverschiebung bei jeder auslaufenden Welle.

Mittels Integration und der Orthogonalitätsrelationen der P_l findet man:

Jede Partialwelle hat damit einen Beitrag _l. Das Maximum tritt natürlich genau dann ein, wenn der Sinus gleich eins ist: _lmax = 4²(2l + 1). Wenn die Phasenverschiebung gleich 0 ist, gilt _tot = 0; es findet also keine Streuung statt.

• Erste Bemerkung:

  Wir berechnen:

  

  Hieraus ergibt sich also das sogenannte „optische Theorem“:

  

• Zweite Bemerkung:

  Als Übung kann man Zentralpotentiale endlicher Reichweite betrachten: V (r) = 0 für r > r₀.

9.2.1 Intermezzo

y

Wenn diese Determinante in irgendeinem Punkt gleich 0 ist, so ist auch die logarithmische Ableitung von y₁ und y₂ gleich:

Theorem:

Sind z1 und z2 Lösungen der Gleichungen z1'' + F1(x)z1 = 0 () und z2'' + F2(x)z2 = 0 () im Intervall (a,b), in denen die Funktionen F1(x) und F2(x) stetig sind (eventuell Unstetigkeiten erster Art, also Sprünge von endlicher Größe), so gilt:

ab = ab(F1 - F2)z1z2 dx

Beweis:

Durch Integration folgt dann die Behauptung.

Korollar:

Es sei F1 = 1-U(x) und F2 = 2-U(x). Sind dann y1 und y2 Lösungen der Gleichung y''+(-U(x))y = 0 zu den Werten 1 und 2, so gilt:

ab = (2 - 1) aby1y2 dx