[next] [prev] [prev-tail] [tail] [up]

9.3 Integraldarstellung

Wir suchen einen Zusammenhang zwischen dl und ^d l, die zu verschiedenen Potentialen V (z) und ^V(z) gehören, aber zum selben Eigenwert E.

[ 2 ] -d- + e- ^U - l(l+-1) y^l = 0 mit e =_ k2 = 2mE-und U =_ 2mV dr2 r2 h2 h2

Mit der asymptotischen Form ^y l ~ sin( ) kr- lp2 +d^l schreiben wir die WRONSKI-Determinante auf:

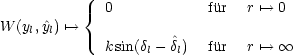
{ 0 f¨ur r '--> 0 W (yl,^yl) '--> k sin(dl-d^l) f¨ur r '--> oo

Es gilt yl = klrl+1, so ergibt sich die WRONSKI-Determinante W(yl,^y l) = 0. Für den zweiten Grenzwert gilt mit x =_ kr -lp 2 und den Additionstheoremen:

^ ^ ^ ^ W ~ k sin(x+ dl)cos(x +dl)- kcos(x+ dl)sin(x+ dl) = ksin(x + dl)cos(-x - dl)+ k cos(x+ dl)sin(-x - dl) = = k sin(x+ dl- x -d^l) = ksin(dl- ^dl)
(9.1)
Mittels des WRONSKI-Theorems finden wir:
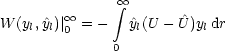
integral oo W (yl,^yl)| oo 0 = - ^yl(U - U^)yldr 0

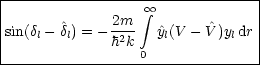
|-------------------------------| | 2m integral oo | |sin(dl- ^dl) = - h2k y^l(V - ^V)yldr| -----------------0---------------

Dies gilt für beliebige Potentiale mit

lim rV^(r) = 0 und lim r2^V(r) = 0 r'-->o o r'-->0

Sie dürfen folglich im Ursprung nicht zu stark konvergieren.

Beispiel:
Betrachten wir den Fall ^V = 0 (d^ l = 0, ^y = krjl(kr)). Dann finden wir:
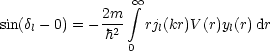
integral oo sin(d - 0) = - 2m rj (kr)V (r)y(r)dr l h2 l l 0

Hier wird dl und yl gesucht. Sowohl die BESSELfunktionen jl als auch das Potential V sind gegeben. Bisher haben wir exakt gerechnet. Nun wollen wir uns aber näher mit der BORNschen Näherung beschäftigen:

Ist V genügend klein, so ist yl(r) ~~ krjl(kr) und dl liegt in der Nähe von Null. Dann gilt:
dl ~~ dlBorn = -2m -2- hk integral 0 oo r2jl2(kr)V (r)dr

Der Fehler ist gering, falls V (r) gegenüber E -l(l+1)h2 -2mr2- fast überall hinreichend klein ist (unverbindlich). Damit ist die BORNsche Näherung bei hohen Energien bzw. großen Werten von l ziemlich gut.

[next] [prev] [prev-tail] [front] [up]