9.6 Bornsche Nherung

Betrachten wir nochmals zur Wiederholung:

integral ( ) ( ) fBorn(k') = ---m-- d3r'exp - ik'.r' V (r')exp ik.r' k 2pk2

ist hierbei der Impuls der einlaufenden Teilchen und ' der Impuls der auslaufenden Teilchen. Hierbei gilt |' | = || und ' = .

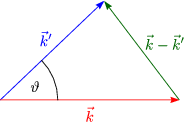
Als Übung soll an dieser Stelle der Zusammenhang | -' | = 4k² sin² gezeigt werden. Für ein rotationssymmetrisches Potential gilt:

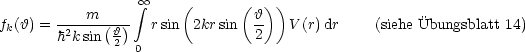
oo ----m----- integral ( (h-)) fk(h) = h2k sin(h-) r sin 2krsin 2 V(r)dr (siehe ¨Ubungsblatt 14) 2 0

Wir betrachten als Beispiel das YUKAWA-Potential V (r) = V ₀:

fk(h) = - 2mV0-----21(h-)----- h2a 4k2sin 2 + a2

Wir betrachten den Übergang zum COULOMB-Potential mit V ₀ = Z₁Z₂e²:

a'-->0 2 V(r) = Z1Z2e2exp(-ar)------> Z1Z2e- r r

a'-->0 ---2mZ1Z2e2---- fk(h) -----> -h2 .4k2sin2(h ) 2

Wir den Streuquerschnitt und die Energie gilt:

s(_O_) = --Z21Z22e4(-)-mit E = h2k2 16E2 sin4 h2 2m