11.4 Lippmann-Schwinger-Gleichung

11.4 LIPPMANN-SCHWINGER-Gleichung

Als erstes suchen wie die GREENsche Funktion F eines Teilchens mit der Energie E = :

h2-( 2) ' ' 2m /_\ + k G(r,r) = d(r - r)

G(,' sei die GREENsche Funktion dieses Operators. Man bezeichnet diese Gleichung auch als HELHOLTZ-Gleichung (Theorie C). Die Greensche Funktion G lautet:

|------------------------------| G ±(r,r') = --m--exp-(±-ik|r--r'|) | | 2ph2 |r- r'| | --------------------------------

Für k = 0 erhält man gerade die POISSONgleichung und deren GREENschen Funktion. Machen wir einen Fourieransatz, sol erhalten wir:

integral integral ( /_\ + k2) G(q)exp(iq.r) d3q = exp(iq.x)d3q

Und daraus wiederum ergibt sich:

|-------------| (- q2 + k2)G(q) = 1 ==> G(q) = ---1---| -------k2--q2--

Damit folgt nun wieder mittels Fouriertransformation G(x):

|--------------| -d3q--exp(iqx)- | 1-exp(±-ik|x| ) | G(x) = (2p)3k2- q2± ie = - 4p |x| | ----------------

Betrachten wir nun wieder unsere ursprüngliche Gleichung:

h2- 2 2m ( /_\ + k )y = Vy

Gesucht ist eine Lösung vom Typ ⁽⁺⁾. Diese Lösung genügt einer Integralgleichung, nämlich der LIPMANN-SCHWINGER-Gleichung:

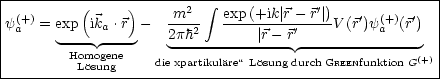
|------------------------ integral ----------------------------| y(+) = exp (ik .r)- m2-- exp-(+ik| r--r'|)V (r')y(+)(r') | | a ---- a---- 2ph2-------|r---r'----------a---- | | Homogene (+) | ---------L¨osung-----die xpartikul¨are“-L¨osung durch GREENfunktion-G|

Diese Gleichung ist exakt für alle Werte r. Was gilt nun asymptotisch, also für r' » r (siehe Multipolentwicklung, Theorie C):

[ r.r' r'2]12 r |r- r'|= 2 1- 2--2-+ -2- ~~ r-- .r' r r r

Mit = k ergibt sich:

exp(ik|r- r'|) exp(ikr) --------'--- ~~ -------exp(-ik.r') |r- r| r

Schließlich gilt folgende Näherungslösung:

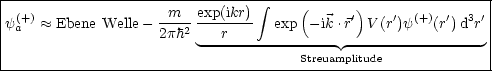
|--------------------m---exp(ikr) integral ----(------)----------------| |y(a+) ~~ Ebene Welle----2 ------- exp -ik .r' V (r')y(+)(r')d3r'| | 2ph --r-------------- ----------------- | --------------------------------------Streuamplitude--------------|

11.4.1 BORNsche Reihe für die stationäre Streuwelle

Man löst die LIPPMANN-SCHWINGER-Gleichung durch Iteration:

1.Ordnung: $integral y = exp(ik .r)+ G(r,r')V (r')exp(ik .r')d3r' 1 a a$
2.Ordnung: $integral y = exp (ik .r)+ G(r,r')V (r')y (r')d3r' 2 a 1$

Für die BORNsche Reihe gilt:

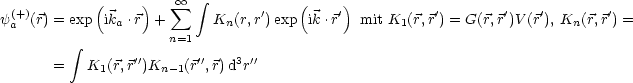( ) sum oo integral ( ) y(+a)(r) = exp ika .r + Kn(r,r')exp ik.r' mit K1(r,r') = G(r,r')V (r'), Kn(r,r') = n=1 integral '' '' 3 '' = K1(r,r )Kn -1(r ,r)d r

(11.1)

a bis n = 2:

y = exp(ikr)+ GV exp(ikr)+ GVGV exp(ikr)

T_ab <_b|V |_a⁽⁺⁾> ist damit eine Entwicklung nach Potenzen von V . Bei der BORNschen Näherung T_ab^(B) bricht man die Entwicklung ab bei n > 2. Wir schätzen den Fehler bei hohen Energie ab:

| ( )| (y(r)) =_ ||y(a+)(r)- exp ika .ra ||« 1 f¨ur r mit V (r) /= 0

Für die Streuphasen im Falle ka » 1 gilt:

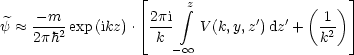
|_ _| - m 2pi integral z ( 1 ) y ~~ ---2 exp (ikz). |_ - V(k,y,z')dz'+ -2 _| 2ph k - oo k

|y| ~~ -m--2p2a|V0|==> |V0|« h2k- 2ph2 k ma

V ₀ gibt eine mittlere Tiefe und a die Reichweite des Potentials an.

Resumé:

Es sei H = H₀ + V und |_n> eine ebene Welle mit Wellenvektor , wobei <|_n> = exp(i_n ^.) gilt. Die ein- und auslaufenden stationären Streuzustände bezeichnen wir mit |_n^(-)>, |_n⁽⁺⁾>. Damit gilt dann: