[next] [prev] [prev-tail] [tail] [up]

11.6 Greensche Funktion der Schrödingergleichung

Die freie Schrödingergleichung für H0 lautet:

(E - H )| f > = 0 mit H =-p2 0 0 2m

Was uns aber interessiert, ist die Schrödingergleichung für H = H0 + V :

(E - H0)|y> = V |y>

Formal ergibt sich dann hieraus:

-1 |y> = (E + H0) V |y >+ |f>

Leider existiert der Ausdruck (E -H0)-1 nicht. H0 -E ist also nicht invertierbar, da 0 ein Eigenwert von H0 - E ist! Infolgedessen definieren wir eine Resolvente G0(z) := (z - H0)-1 mit z (- C; G0(z) ist definiert, falls z kein Eigenwert von H0 ist.

G(± )(E) = lim G (E ± ie) = lim (E - H ± ie)-1 0 e'-->0+ 0 e'-->0+ 0

In der Ortsdarstellung können wir schreiben:

m exp (±ik| x - x') V~ 2mE- <x |G(±)(E)|x'> = ----2 --------'-----=: G(±0 )(x,x') mit k =--2-- 2ph |x- x | h

G0(±) sind GREENsche Funktionen des freien Schrödingergleichung:

2 ( ) h-- /_\ + k2 G(0±)(x,x') = d3(x- x') 2m

Betrachten wir die LIPPMANN-SCHWINGER-Gleichung:

|y(+)> = |fa >+ G(+)(E0)V |y(+)> a 0 a

Analog gilt:

|y(a-)> = |fa >+ G(0-)(E0)V |y(-a )>

Die Resolvente des vollen Hamiltonoperators lautet:

G(z) := (z- H) -1

G(±)(E) = lim (E ± ie- H)- 1 e'-->0+

|--(+)----------(+)---------| -|ya->-=-|fa>-+G---(Ea)V-|fa>-|

Diese Beziehung wollen wir überprüfen, indem wir von links mit Ea - H multiplizieren:

(+) (+) (Ea - H)|ya > = (Ea--H0)-|fa> -V |fa>+ (Ea---H) G-(Ea) V|fa> = 0 =0 =1

Dies ist eine wahre Aussage.

G(+)(Ea)V |fa> = G(0+)(Ea)V |y(+a)> = G(+0)(Ea)V |fa>+G(+0) (Ea)V G(+)(Ea)V|fa>

|---------------------------| |G(+)V = G(+)V + G(+)V G(+)V | ----------0-------0----------

11.6.1 Übergangsoperator

<fb|T|fa> = <fb| V |y(+a)> = <fb|V|fa>+ <fb| V G(+)V|fa>

Der Übergangsoperator T ist definiert durch:

|---------------| |T = V +V G(+)V | -----------------

Damit haben wir folgende iterative Lösung:

(+) (+) (+) T = V + V G0 V +V G0 VG V

(+) (+) (+) T = V + VG 0 V + V G0 VG 0 V + ...

Satz:
Es gilt T - T† + 2piT†T = 0 und T - T† + 2piTT† = 0.
Beweis:
T = V + V G(+)V und T† = V + V (- )V

( ) ( ) ( ) T -T† = V G(+)- G(-) V = V ----1------ ----1----- V = V E---H---ie---E-+-H---ie V E - H + ie E - H + ie (E - H)2 + e2

Wir führen den Grenzübergang ie'-->0 formal durch:

T - T† = V .(- 2pi) .d(E - H)V

Aufgrund der Vollständigkeit der Basis können wir ein Einselement 1 einschieben:

sum 1 = (2p)3 |y(-n)><y(-n )| n

† 3 sum (-) (-) <fb| T - T |fa> = (2p) <fb|V|yn >d(E - En)<yn |V |fn >.(- 2pi) n

Wir führen einen weiteren Grenzübergang „Summe '--> Integral“ durch:

sum integral (2p)3 '--> --1-3 |y(a-)><y(n-)d3kn n (2p)

--1-3d3k = r(E) dE d_O_ (2p)

Damit erhalten wir weiter:

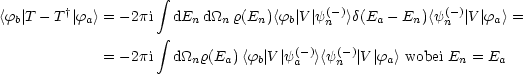integral † (- ) (-) <fb|T - T | fa> = -2pi dEn d_O_n r(En)<fb| V |yn >d(Ea - En)<yn |V |fa > = integral (- ) (- ) = -2pi d_O_nr(Ea) <fb| V |y a ><yn |V|fa> wobei En = Ea
(11.2)
<fb| V |y(- )> = <y(+)|V|fn> = <fb| T †| fn> n b

<y(n-)|V |fa > = <fn| V |y(+a)> = <fn |T|fa>

Schlußendlich erhalten wir unsere Aussage:

|-----------------| -T---T† =---2piT†T|

Satz:
Der S-Operator S := 1 - 2piT ist unitär.
Beweis:
Nach unserem letzten Satz gilt:
S†S = 1+ 2piT†- 2piT +4p2T †T= 1 --------=0---------

Für die S-Matrix gilt <fb|S|fa> = <yb(-)|ya(+)>.

[next] [prev] [prev-tail] [front] [up]