12.1 Experimentelle Entdeckungen

• Paritätsverletzung:

  Wir betrachten einen massiven Einteilchenzustand _,. Hierbei gilt für den Paritätsoperator P_, = _,, wobei man als intrinsische Parität bezeichnet. Die starke Wechselwirkung ist paritätserhaltend; also kommutiert H = H₀ +H_I^stark mit P: [P,H_I^stark] = 0. Für die Teilchen ^±, ⁰ gilt = -1; man bezeichnet diese als pseudo-skalare Teilchen.

• Man hat zwei seltsame Spin-Null-Teilchen gefunden, welche man als ^± und ^± bezeichnet hat.

  Zerfallskanal	Masse [me]	Zerfallszeit t [s]
  ++0	966,7 ± 2,0	1,21 ± 0,002 . 10-8
  +++-	966,3 ± 2,0	1,19 ± 0,05 . 10-8

  Die Unterschiede zwischen diesen Teilchen sind sehr klein. Aus dem Zerfall = erhält man eine intrinsische Parität () = -1 und aus folgt () = +1. Einerseits sind die Teilchen und in ihren physikalischen Eigenschaften fast gleich, andererseits unterscheiden sie sich aber in der intrinsischen Parität. LEE und YANG fanden im Jahre 1956 eine Lösung für dieses Problem. In bezug auf die schwache Wechselwirkung ist die Parität nicht erhalten; es gilt also [H_I^schwach,P]0 und ^± = ^±.

• Experiment von WUETAL im Dezember 1956

  In diesem Experiment wurde der Zerfall ⁶⁰Co⁶⁰Ni + e^- + _e untersucht. Hierbei gilt und .

  

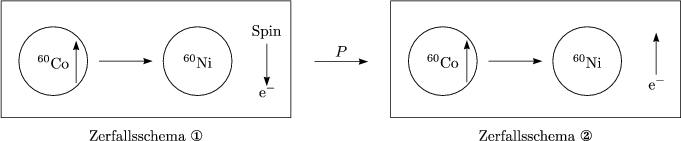
  Das erste Schema wurde tatsächlich von WUETAL beobachtet, aber das zweite nicht. Bei der schwachen Wechselwirkung kann also die Parität verletzt werden.

  

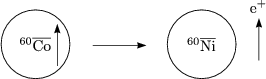
  Wenn man nun eine CP-Transformation durchführt, könnte man folgenden Zerfall beobachten:

  

  Im Jahre 1964 wurde aber herausgefunden, daß CP im K⁰K⁰-System verletzt ist. Es liegt aber immer noch CPT-Erhaltung vor!

  

  [next] [front] [up]