4.3 Mischphasen in der Thermodynamik

4.3.1 Partielle molare Größen

Frage:

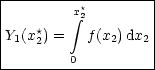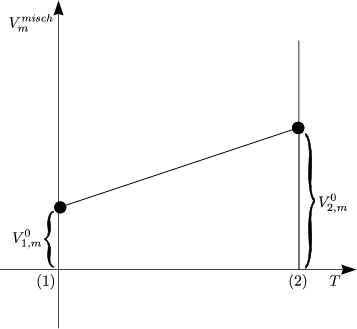
Wir betrachten eine homogene Phase aus K Komponenten. Wie setzen sich die molaren thermodynamischen Größen dieses Systems aus den Beiträgen der einzelnen Komponenten zusammen?

Beispiel:

Wir betrachten eine Mischung aus C₆H₆ (l) + C₆H₅CH₃ (l). Wir nehmen an, daß es sich um eine ideale Mischung handelt, das heißt, daß die Wechselwirkungen 1 : 1,1 : 2,2 : 2 gleich sein sollen.

Energetische und entropische Größen sind gleich, wenn sie sich ideal mischen.
Mischungsvolumen $V = n1VQ + n2VQ |:---1--- 1,m 2,m n1 + n2$

$VMischung = x1VQ + x2VQ m 1,m 2,m$

Wir betrachten wiederum eine ideale Mischung, der welcher also die Wechselwirkungen 1-1, 1-2, 2-2 gleich sein sollen. Des weiteren sei vorausgesetzt, daß _1-1,_1-2,_2-2 äquivalent seien.

Vm(x2) = x1VQ1 + x2VQ2 = (1- x2)VQ1 + x2V2Q

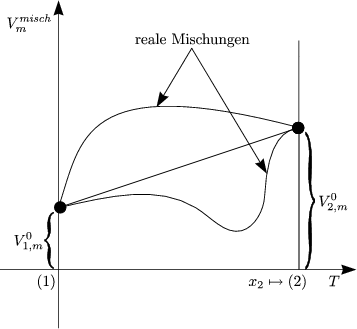
In realen Mischungen können die extensiven Mischungsgrößen Y _m $/\ =$ V _m, G_m, F_m, S_m, H_m, U_m, ... von idealen Werten abweichen.

Problem:

Wie ist Y _m aus Einzelbeiträgen der Komponenten darstellbar, speziell für binäres System aus (1) und (2)?

Antwort:

Wir formulieren dies beispielsweise für Volumen V . V ist eine Zustandsgröße: V (T,p,n₁,n₂), läßt sich also als partielles Differential schreiben:

( ) ( ) ( ) ( ) dV = @V- dT + @V- dp+ @V-- dn1+ @V-- dn2 @T p,n1,n2 @p T,n1,n2 @n1 T,p,n2 @n2 T,p,n1

Da p und T konstant sind, fallen die ersten beiden Ausdrücke weg:

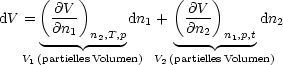
( ) ( ) dV = @V-- dn1 + @V-- dn2 -@n1 n2,T,p -@n2 n1,p,t V1(partiellesVolumen) V2(partiellesVolumen)

Daraus ergibt sich also mit den partiellen Volumina V ₁ und V ₂:

V = V n + V n |.---1--- 1 1 2 2 n1 + n2

|---------------| Vm--=-V1x1 +-V2x2

Fazit:

Mischungsgrößen sind allgemein aus den partiellen Größen Y _m =

_ix_iY _i anzugeben.

Frage:

Wie ist Y _i aus der integralen Größe Y _m zu bestimmen?

Lösung:

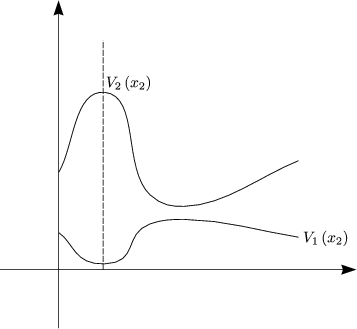
Der Beweis ist einfach, aber länglich!

Tangentenmethode:

Frage:

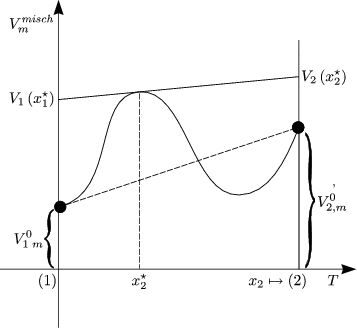
Sind V ₁(x₂) und V ₂(x₂) (siehe Bild) linear unabhängig?

Antwort:

Nein! Die Antwort gibt die GIBBS-DUHEMsche Gleichung.

Beweis:

Es gelte k = 2. Da p und T konstant sind, gilt Y = Y ₁n₁ + Y ₂n₂. Hierbei ist wichtig, daß die Y _i(x_i) keine Konstanten sind. Daraus folgt nun durch Differentiation: