4.4 Thermodynamik idealer Mischungen

[next] [prev] [prev-tail] [tail] [up]

4.4 Thermodynamik idealer Mischungen

{ } DVm = 0 ==> makroskopische Definition idealer Mischung DHm = 0

Wobei beispielsweise für V _m definiert ist als:

sum sum Q Q DVm = Vm,nach- Vm,vor = Vixi- Vi xi i i

Wie groß ist nun S zum Beispiel für zwei ideale Gase?

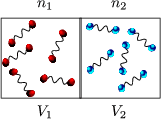
Wir gehen vom 1. und 2. Hauptsatz aus:

dU = dq- pdV = TdS - pdV

Wie wir schon in Kapitel 2 gesehen haben, ist für ein ideales Gas dU = 0.

dS = -pdV = nRT-dV- T T V

Durch Integration erhalten wir:

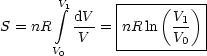
V integral 1 |----(---)-| S = nR dV- = nR ln V1 | V V -------V0--- 0

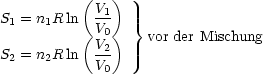
( ) V1 S1 = n1R ln (V0 ) } V2 vor der Mischung S2 = n2R ln V0

Nach der Mischung: (V1 + V2)

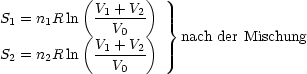
( ) S1 = n1R ln V1 +-V2 } ( V0 ) nach der Mischung S2 = n2R ln V1 +-V2 V0

Die Entropiedifferenz berechnet sich nun durch Subtraktion der Entropien vor und nach dem Mischvorgang:

sum sum (V1 + V2) (V1 + V2) DS = niSi,nach- niSi,nach = n1R ln ---V1-- + n2Rln --V2--- i i

Mit = = und der analogen Beziehung für x₁ ergibt sich:

2 --DS--- =_ DS = - R sum x lnx n1 + n2 m i=1 i i

|-------------------------------------------| | sum @G- | |DGm = RT xilnxi und Dmi = @xi = RT lnxi| --------------------------------------------

Frage:

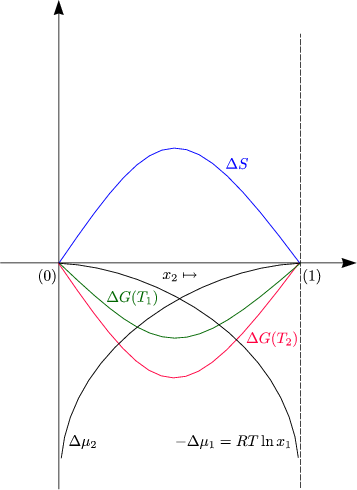
Wir groß ist

V _i für eine ideale Mischung?

( ) DV = @Dmi- =_ 0 etc. i @p

Dmi = RT ln xi

Für x_i1 gilt _i_i.

|----------------| mi = mQ+ RT lnxi | ------i-----------

Dies ist die Definition für eine ideale Mischung.

Frage:

Wie sieht es mit realen Mischungen aus?

DH /= 0,DV /= 0-- > m /= mQ + RT lnx i i i

Der Ansatz ist nun _i = _i + RT lnx_i + Korrektur = _i + RT lnx_i + RT ln_i mit dem Aktivitätskoeffizienten _i und der Aktivität a_i = x_i_i. Fassen wir zusammen:

Chemisches Potential in idealer Mischung: $|-----Q----------| mi =-mi +-RT-lnxi-$
Chemisches Potential in realer Mischung: $|----------------| mi = mQi + RT lnai| ------------------$
a_i = _ix_i nennt man Aktivität und _i bezeichnet man als Aktivitätskoeffizient. Für eine ideale Mischung oder Lösung ist _i 1, sonst aber gilt _i1.

[next] [prev] [prev-tail] [front] [up]