1.2 Typischer Verlauf von Potentialkurven

1.2.1 Intermolekulare Wechselwirkung beim Leonard-Jones-Potential

Grobe Näherung für Potentialkurve:

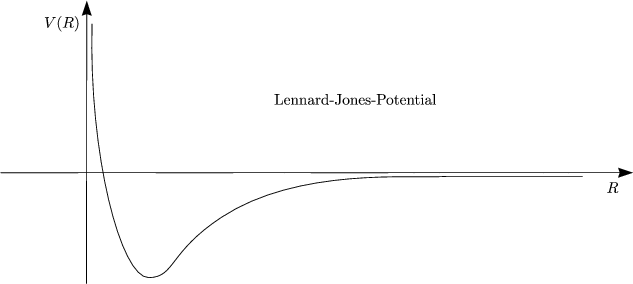
Näherung von V (R) durch harte Kugel Potential V _hs (hard sphere potential)

Frage:

• Verdünnte Gase

• Ideales Gas wenn zusätzliches Volumen der Molekeln gleich 0

Wir kehren nun zu dem Problem zurück, wie sich das Volumen eines Gases in Abhängigkeit von Druck und Temperatur verändert. Wir suchen also die Funktion V = V (p,T). Ein Gedankenexperiment (Fahrradpumpe) soll uns weiterhelfen:

1. P wenn T = const.

   Wobei die Einheit des Druckes 1bar ist und 1bar = 10⁵ Pa mit 1Pa = 1

2. V T wenn p=const.

   Die Einheit der Temperatur ist (T + 273,15)K; Kelvin-Skala

3. V n wenn p,T=const.

   n Molzahl bzw. Molares Volumen bzw. Molvolumen

Résumé:

p ^. V = n ^. R ^. T

Dies ist die Zustandsgleichung idealer Gase mit der Gaskonstante R = 8,31 und dem molaren Volumen V _m = 22,4 bei 273,15K und 1atm. Man kann die Funktion V (p,T) folgendermaßen mittels der partiellen Ableitungen als totales Differential schreiben:

Läßt sich dV als totales Differential schreiben, so gibt es eine Potentialfunktion, die wegunabhängig ist. Das heißt:

Frage:

Unter welchen Bedingungen dV ein totales Differential?

Antwort:

Es gilt der Schwarz’sche Satz, welcher angewandt auf V (p,T), folgendermaßen lautet:

p = T

Zurück zum Mikroskopischen:

Frage:

Antwort:

Wir betrachten folgendes Modell:

1. »
2. Stöße von Molekeln untereinander oder mit Wand gehorchen den klassischen Gesetzen der Mechanik d.h. Impuls- und Energieerhaltung gelten.
3. Die Molekeln bewegen sich regellos.

Der Impulsübertrag für eine Molekel i ergibt sich durch:

Durch Summation über N erhalten wir den Impulsübertragung auf Wand senkrecht zu x für N Molekeln: Daraus ergibt sich dann der Druck auf Wand senkrecht zu x:

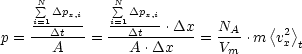
Aufgrund der unregelmäßigen Bewegung der Molekeln können wir folgenden Zusammenhang zwischen der mittleren Geschwindigkeit <v> und den jeweiligen gemittelten Komponenten <v_x>, <v_y> und <v_z> angeben:

Fassen wir unsere Erkenntnisse zusammen:

1. Zustandsgleichung für ideale, verdünnte Gase:

   p = p(V,T) ist eine Funktion von mehreren Variablen. Eine solche Funktion läßt sich anschaulich als eine Fläche im Raum darstellen. Läßt sich eine Funktion als totales Differential schreiben, so ist dV wegunabhängig.

2. Frage: mikroskopische Interpretation von Größen wie z.B. p oder T