7.2 Geschwindigkeitsverteilung

• Qualitativ:

  Wahrscheinlichkeit N_A, [v,v + dv]

  

• Quantitativ:

  Wie groß ist F(v)?

  

7.2.1 Maxwell-Ansatz

Schließlich läßt sich die Gesamtwahrscheinlichkeit durch Integration über alle möglichen Geschwindigkeiten finden; diese muß gerade den Wert 1 haben:

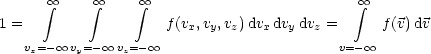
Die Maxwell-Annahme ist nun, daß f(v_x), f(v_y) und f(v_z) nicht gekoppelt sind, da das Gas isotrop ist. Diese lassen sich also separat betrachten. Wir nehmen an, daß sich f() somit als Produkt dreier unabhängiger Funktionen bezüglich einer einzigen Geschwindigkeitskomponente schreiben läßt:

Dann wenden wir den Logarithmus auf obige Gleichung an:

Wir leiten die Funktion nach v_x ab und erhalten:

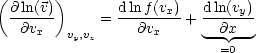
Mit v = ergibt sich nun:

Wir multiplizieren das ganze mit durch:

Durch Integration dieser Differentialgleichung erhalten wir:

Des weiteren werten wir die Normierungsbedingung aus:

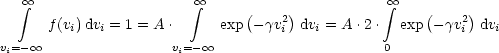
Dies funktioniert auch analog für v_x und v_z.

7.2.2 Druck in der kinetischen Gastheorie

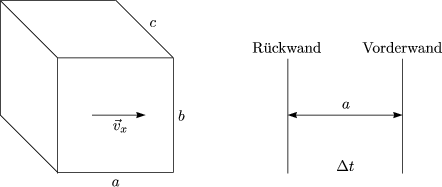
Der übertragene Impuls berechnet sich dann durch p = (v_x) = 2mv_x. Wir berechnen außerdem die Kraft als zeitliche Impulsänderung:

Wir dividieren F durch die Fläche b ^. c, womit der Druck resultiert:

Der Druck, den ein Teilchen i erzeugt, lautet p_i = . Durch Summation über alle Teilchen N erhalten wir den Gesamtdruck:

Mit der mittleren quadratischen Geschwindigkeit

läßt sich dies schreiben als:

Es gilt, da es sich um ein isotropes Gas handelt und somit der Betrag der Geschwindigkeit unabhängig von der Richtung ist:

Das ideale Gasgesetz lautet, wie wir wissen pV = nRT;

Damit gilt für die mittlere quadratische Geschwindigkeit, wobei M die Molmasse ist:

Allgemein gilt für den Mittelwert eine Funktion g(x):

Wir wenden dies auf unser Problem an:

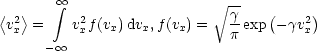
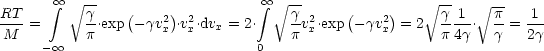
Damit erhalten wir die eindimensionale MAXWELL-BOLTZMANN-Geschwindigkeitsverteilung:

7.2.3 Dreidimensionale Geschwindigkeitsverteilung

(7.1)

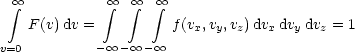
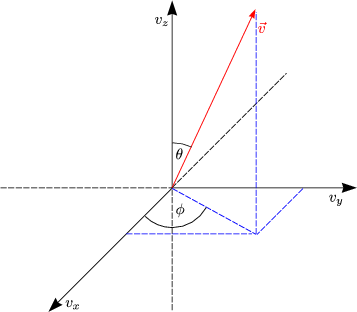
Zur Berechnung des Integrals führen wir Kugelkoordinaten ein:

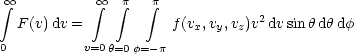
Die Lösung ist:

7.2.4 Temperaturabhängigkeit der Geschwindigkeitskonstanten
(Arrhenius-Gesetz)

Exponentialfunktion Harmonisches Ensemble

7.2.5 Zusammenfassung der Ergebnisse: Maxwell-Boltzmann-Ge schwindigkeitsverteilung

• Maximum bei v_x = 0
• Das Integral über f(v_x)dv_x von v_x = - bis v_x = muß den Wert 1 ergeben.
• Die Herleitung von F(v) bedeutet Koordinatentransformation (kartesische Koordinaten Kugelkoordinaten)

  

  

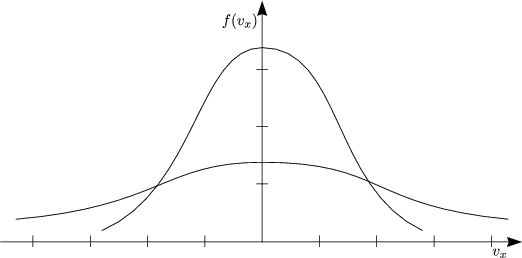
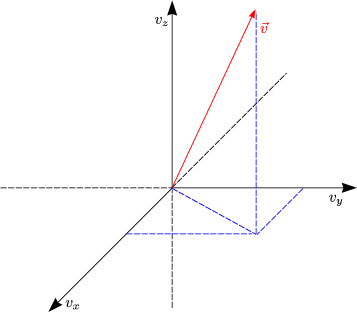
  Die Wahrscheinlichkeit, ein Teilchen zu finden mit v zwischen v und v+dv (irgendwo gerichtet im Raum), berechnet sich folgendermaßen:

  

  

  1. p ist in F(v) nicht vorhanden
  2. T-Abhängigkeit: T^- exp
  3. Verteilungsfunktion ist massenabhängig

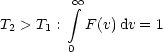
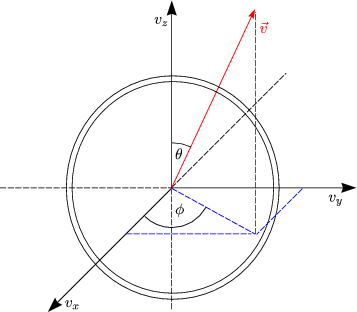
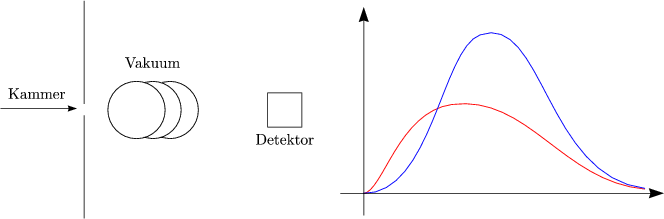
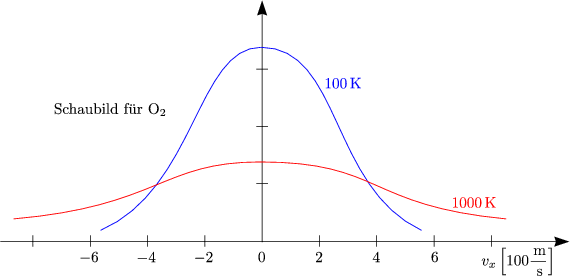
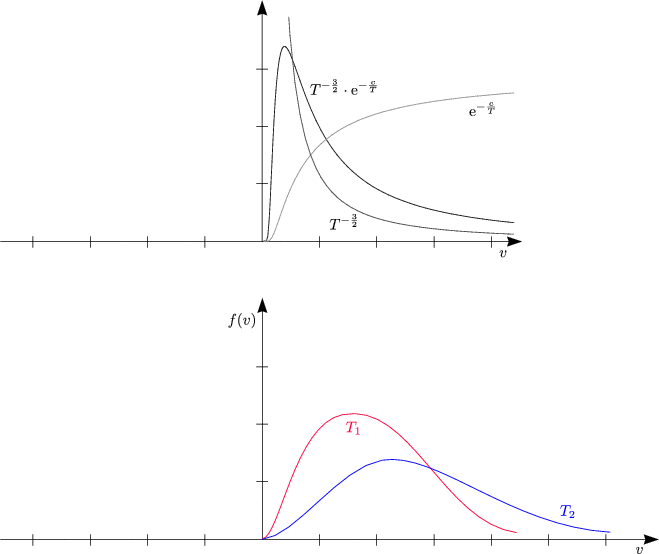
  Das Schaubild zeigt das Aussehen der Verteilungsfunktion bei zwei verschiedenen Temperaturen T₁ und T₂.

  

  Das folgende Schaubild zeigt die Verteilungsfunktion für zwei verschiedene Gase, nämlich für Sauerstoff und Wasserstoff.

  

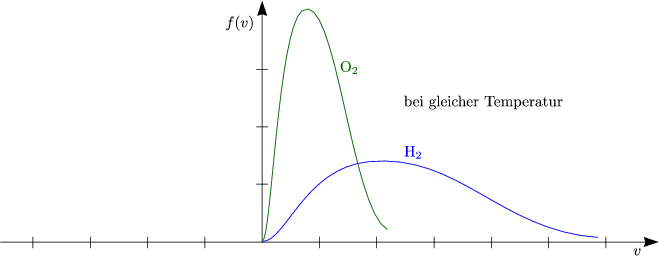
  Wir suchen jetzt eine Verteilungsfunktion der Relativgeschwindigkeiten bei Stoß zwischen A und B.

7.2.6 Mittelwerte der dreidimensionalen Maxwell Boltzmann Geschwindigkeitsverteilung

• Wahrscheinlichste Geschwindigkeit

  Diese erhält man als Extremwert durch Ableiten der Geschwindigkeitsverteilung und Nullsetzen:

  

  m ist hierbei die Teilchenmasse und M die molare Masse.

• Mittlere Geschwindigkeit:

  Diese berechnet sich durch Integration:

  

  (v ist hier kein Vektor!)

  
  

• Mittleres Geschwindigkeitsquadrat:
  

Beispiele:

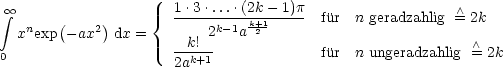
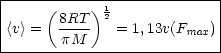
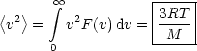
Gas
H2	1692
He	1204
N2	454
Hg	170

Es gilt k^bimolekular |v_rel|. |v_rel| kann durch folgendes zunächst furchterregendes Integral berechnet werden:

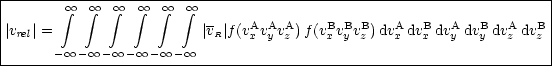
Die genaue Lösung findet sich in MOORE/HUMMEL: Physical Chemistry.

_AB ist hierbei die reduzierte Masse der beiden Teilchen:

Wir haben jetzt in unserer Formel eine T-Abhängigkeit aber noch kein exp.