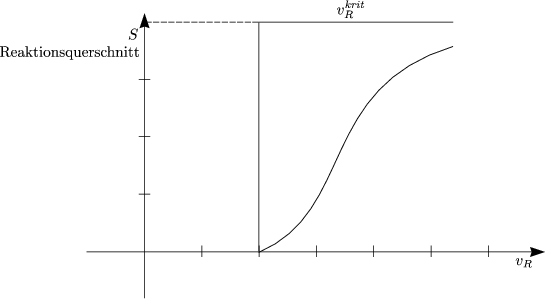
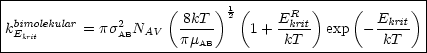[next] [prev] [prev-tail] [tail] [up]

7.3 Berechnung der Anzahl der Stöße mit mehr als Ekrit(= Ea)

Aus der Verteilungsfunktion kann man f(vR) herleiten. Für die Anzahl der Stöße mit vR zwischen vR und vR + dvR (auf Volumen gerichtet) erhält man:

--1-- --1- [A(t)] = [A]0 + 2k2t

( ) ( )3 ( )1 ( ) d Zges = ps2 N 2 [A][B] mAB-2 2- 2 exp - mABv2R- v3dv = ps2 N 2 (v f(v )dv )[A][B] DV AB AV kT p 2kT R R AB AV R R R

Wir nehmen jetzt kritische Stoßenergie Ekrit an (jeder Stoß mit dieser Energie und darüber reagiert), d.h. wir integrieren von d( ) Zges DV ab vkritR bis vR = + oo . Hierzu benötigen wir die Berechnung des folgenden Integrals:

| integral -----(---)---| | x3exp ax2 dx| -----------------

Dazu führen wir folgende Substitution durch:

x2 = u, du-= 2x ==> du = 2xdx dx

integral integral integral ( integral ) 3 ( 2) du- 1 1 [u- ] 1- x exp ax dx = uxexp(au).2x = 2 u exp(au) du = 2 a exp(au) - a exp(au) du = 1(u 1 ) 1 ( 1 ) 1 ( 1) = - -exp (au) - -2 exp(au) = -- u(au)- --eau = --exp(au) u- -- 2 a a 2a a 2a a
(7.2)
Rücksubstitution durch x ergibt:
( ) ( ) 1-exp(au) u- 1- = 1-exp(ax2) x2- 1- 2a a 2a a

Ausklammern von -1 -- a ergibt:

( ) 1-exp(ax2). --1 .[1 - x2 .a]= --1-exp (ax2)(1 - x2 .a) 2a a 2a2

Einsetzen der Grenzen ergibt:

oo integral [ ( ) ] oo x3exp (ax2)= -1 exp(ax2). - 1- .[1- x2 .a] = -1-exp(av2 )(1- v2 .a) 2a a vkrit 2a2 krit krit vkrit

Mit a = -mAB 2kT- und den jeweiligen Vorfaktoren erhält man nun für die Geschwindigkeitskonstante:

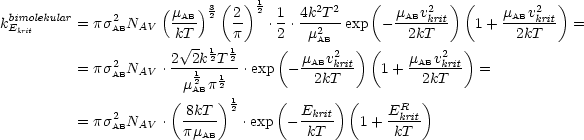(mAB)32 (2 )12 1 4k2T2 ( mABv2 )( mABv2 ) kbiEmkroitlekular= ps2ABNAV kT-- p- .2 .-m2---exp - --2kkTrit 1+ -2kTkrit- = V~ - 1 1 ( AB )( ) = ps2 N .2--2k2T2-.exp -mABv2krit 1 + mABv2krit = AB AV m12ABp12 2kT 2kT ( )12 ( )( R ) = ps2ABNAV . -8kT- .exp -Ekrit 1+ E-krit- pmAB kT kT
(7.3)
|-----------------------------------------------------| | ( 8kT )12 ( ER ) ( E ) | |kbEimkoritlekular = ps2ABNAV ----- 1+ --krit- exp - -krit- | -----------------------pmAB---------kT----------kT----

PIC

[next] [prev] [prev-tail] [front] [up]