2.3 Boltzmannverteilung und spezifische Wrme von Gasen und Festkrpern

2.3 Boltzmannverteilung und spezifische Wärme von Gasen und Festkörpern

2.3.1 Boltzmannverteilung

Gegeben sei ein isoliertes System (GAS, FLÜSSIGKEIT, FESTKÖRPER), d.h. die Gesamtenergie E des Systems ist konstant. Des weiteren sei das System zusammengesetzt aus Molekeln.

Frage:

Wie verteilen sich N_A Molekeln auf die molekularen Energiezustände, so daß E resultiert bei Energieaustausch zwischen den Molekeln?

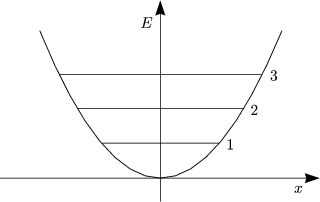
Beispielsweise gäbe es einen Energiefreiheitsgrad: _vib = h. Gegeben sei die makroskopische Energie E Es stellt sich nun die Frage, wieviele Molekeln N_i die Energie _i haben.

n1 n2 n3 ... ni ... e1 e2 e3 ... ei ...

Unter Nebenbedingung:

N_A = _in_i
E = _in_i_i

Beispiel:

N = 3 Molekeln

E = 3.hw

Welche Verteilungen der 3 Molekeln auf die erlaubten Energiezustände

_i sind möglich? Insbesondere: Welche Verteilungen sind am häufigsten realisierbar und damit am wahrscheinlichsten?

Konkretes Beispiel:

N = 3 Molekeln;V = const.;E = 3hn(= 3hw)

( ) Die e sind diskrete Werte, d.h. beispielsweise f¨ur die Schwingung: e = hw v+ 1 i vib 2

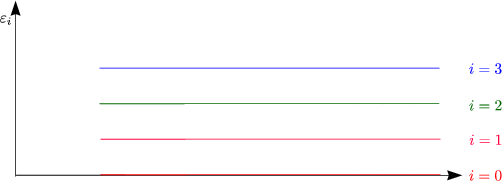
Welche Verteilungen der Molekeln (3) auf

_i sind möglich? Welche Verteilung tritt am häufigsten auf und ist dann die wahrscheinlichste?

Die Annahme ist, daß Molekeln unterscheidbar seien: (a,b,c).

Lösung:

1.Fall: Jede Molekel in v = 1 $E = 0(v = 0)+ 3.hn + 0(v = 2)+ ...= 3hn$

$W (n0[0],n1[3],n2[0],...) = 1$
2.Fall: $W (n0[2],n1[0],n2[0],n3[1]) = 3$
3.Fall: E = 3h $W (n0 = 1,n1 = 1,n2 = 1,nn>2 =_ 0) = |2.3|= 6 Mo¨glichkeiten$

Zusammenfassung:

Größtes W, wenn verschiedene _i besetzt werden
W(n₁,n₂,...) = 3!

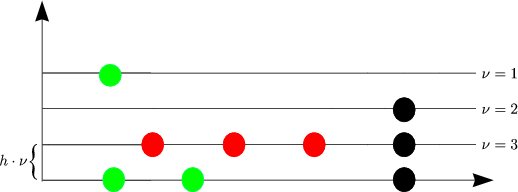
Verallgemeinerung auf N_A Molekeln: Die Anzahl der Möglichkeiten, N_A verschiedene Objekte auf _i zu verteilen, ist N_A!. Wenn in einem _i (Kasten) n_i Molekeln sitzen, gilt:

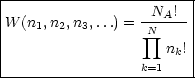
|-----------------------| | -NA!--| |W (n1,n2,n3,...) = N prod | | nk!| ------------------k=1----

Was ist die wahrscheinlichste Verteilung? Diejenige, bei der W als Funktion von N_i war!

Lösung: ______ Extremwertaufgaben mit mehreren Variablen n₁, n₂, n₃, n₄, ..., n_i

W (ni) = max, wenn ni = const. exp(- e,b)

2.3.2 Der Boltzmann-e-Satz

Frage:

Was bedeutet die Konstante vor der Exponentialfunktion bzw. die Konstante

Antwort:

Zur Konstante :
hat die Dimension von 1/Energie; genauer gilt = .
Zur Konstante vor Exponentialfunktion:
Die Nebenbedingung ist, daß die Summe aller Molekeln n_i die Gesamtzahl der Molekeln ergeben muß:
$sum ni = NA i$

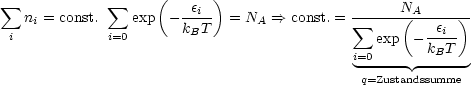
$sum sum ( ) ni = const. exp ---ei- = NA ==> const. = sum ----N(A-----)- i i=0 kBT exp - -ei- i=0 kBT q=Zustandssumme-$
$n exp(- -ei-) p(ei) = -i-= sum ----(kBTe--)- NA exp -kBiT- i=0$

$( e1023) n1023= exp----kT--- NA q(V,T )$
Man kann p(_i) nun folgendermaßen interpretieren:
- Es handelt sich um die Wahrscheinlichkeit, daß ein Zustand mit _i besetzt ist.
- Es ist der Bruchteil von Molekeln, die im Zustand mit der Energie _i sitzen.
$( ) ni exp---ekiT- ( De-) nj = exp(- ej)= exp(- (ej- ei)kT ) =_ exp -kT kT$

Beispiele:

Wir wollen makroskopische thermodynamische Größen (z.B. U(V,T),C_V(T) etc.) aus mikroskopischen Informationen zur Energiequantelung

_i mit BOLTZMANN berechnen. Wir betrachten im folgenden ein 2-Niveau-System (

₁,

₂).

Frage:

Welchen Beitrag liefern diese beiden Energiefreiheitsgrade zu C_V?

Antwort:

Wir müssen U_m(V,T) berechnen.

C_V =

Wir berechnen nun die innere Energie mittels der uns bereits bekannten Beziehungen:

( -e1) ( e2) ( ( e1)) <ei> = n1-.e1+ -n2.e2 = exp--kT- .e1+ exp---kT-.e2 = e1 +-e2-exp(--e1kT) NA NA q q 1 + exp - kT-

De = (e2- e1)

Daraus ergeben sich:

-@- Um(V,T ) = NA <ei> und CV(T ) = @T (<ei>)

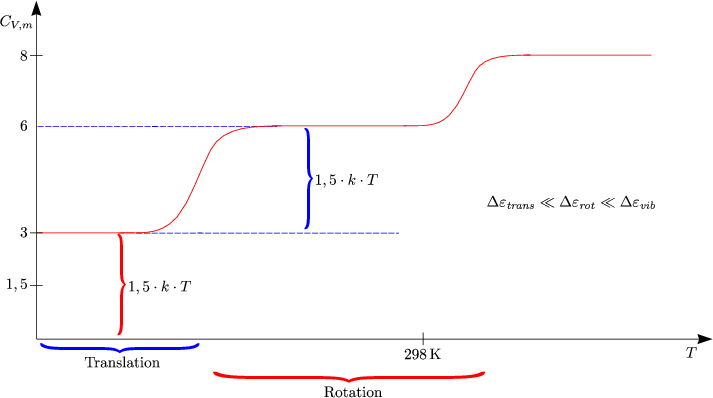
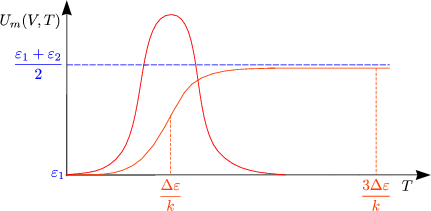
Diskussion von U(V,T) und C_V(T):

T0: U_m(T) = N_A_i
T: U_m(T) = N_A (Gleichverteilung)

Das wesentliche Ergebnis ist also, daß bei T » Gleichverteilung vorliegt (klassischer Grenzfall).

Problem:

Spezifische Wärme von Gasen ausrechnen in dem Grenzfall der klassischen Gleichverteilung

Translation: _trans $|---------------------------| | p2x p2y p2z 3 | etrans = 2m-+ 2m-+ 2m- = 2kT | -----------------------------$
3 Energiefreiheitsgrade der Translation mit kT pro Translationsfreiheitsgrad
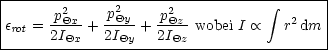
Rotation: _rot $|----------------------------------------| | p2 p2 p2 integral | erot = -Qx- + -Qy-+ --Qz wobei I oc r2dm | ------2IQx---2IQy---2IQz-------------------$
3 Energiefreiheitsgrade der Rotation mit kT pro Translationsfreiheitsgrad
Schwingung: _vib $|------------------------ V~ ---| | p2 1 D | |evib = 2m-+ 2Dx2 mit w = -m | | - - | -------ekin---epot--------------|$

$<e > = 1kT vib$

Frage:

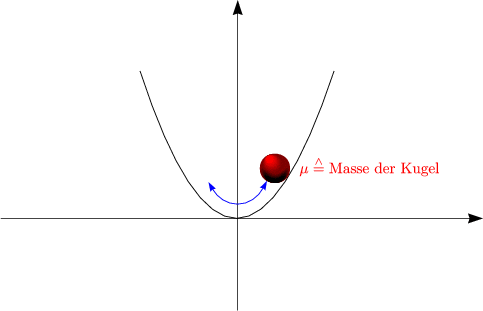
Wieviel Schwingungsfreiheitsgrade hat eine Molekel aus n Atomen (nichtlineare Molekel)?

Betrachten wir zuvor als Beispiel eine nichtlineares Molekel, welche aus drei Atomen besteht:

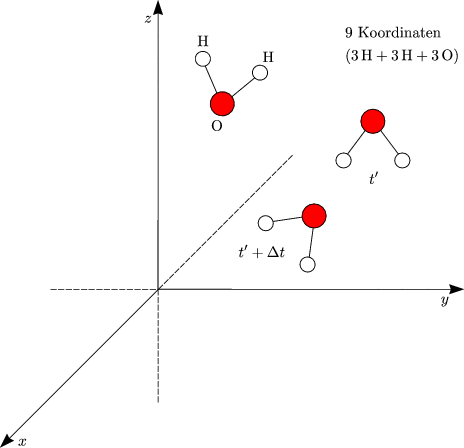
Gehe ins Schwerpunktskoordinatensystem:

Separiere 3 Translationskoordinaten ab.
Separiere 3 Rotationskoordinaten ab.
Es bleiben 3 Angaben für Relativbewegung.

Allgemein gilt:

Nichtlineare Molekel:
Eine nichtlineare Molekel besitzt (3n - 6) Vibrationsfreiheitsgrade.
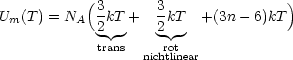
$U (T) = N (3-kT + 3kT +(3n -6)kT ) m A 2 | 2| | trans rot nichtlinear$
Lineare Molekel:
Dagegen besitzen lineare Molekeln 3 Translationsfreiheitsgrade, 2 Rotationsfreiheitsgrade und (3n - 5) Vibrationsfreiheitsgrade.

[next] [prev] [prev-tail] [front] [up]