2.1 Lichtwellen und Quanten

2.1.1 Strahlungsgesetze

Strahlung eines „schwarzen Strahlers“, Hohlraumstrahlung, Temperaturstrahlung:

Die Emission ist unabhängig von chemischer Natur. Sie hängt nur von der Temperatur ab (Beispiel: Ofen, Sonne). Wir machen somit ein Experiment:

Planck hat hergeleitet, daß doe Energien diskret aber nicht kontinuierlich sind. Es liegt eine Quantelung E = n ^. h ^. vor. Eine Anleihe aus der statistischen Thermodynamik ist die Plancksche Strahlungsformel:

h 6,626 ^. 10^-34 Js ist das Plancksche Wirkungsquantum. Die Quantelung der Energie E ist ein Widerspruch zur klassischen Physik.

2 Grenzfälle:

• Rayleigh-Jeans-Gesetz: k_BT » h

  Das Rayleigh-Jeans-Gesetz war ursprünglich klassisch über kontinuierliche Energieverteilung abgeleitet worden. Das Gesetz führt zur „UV-Katastrophe“ bei hohen Frequenzen.

  

• Wiensches Strahlungsgesetz: k_BT « h

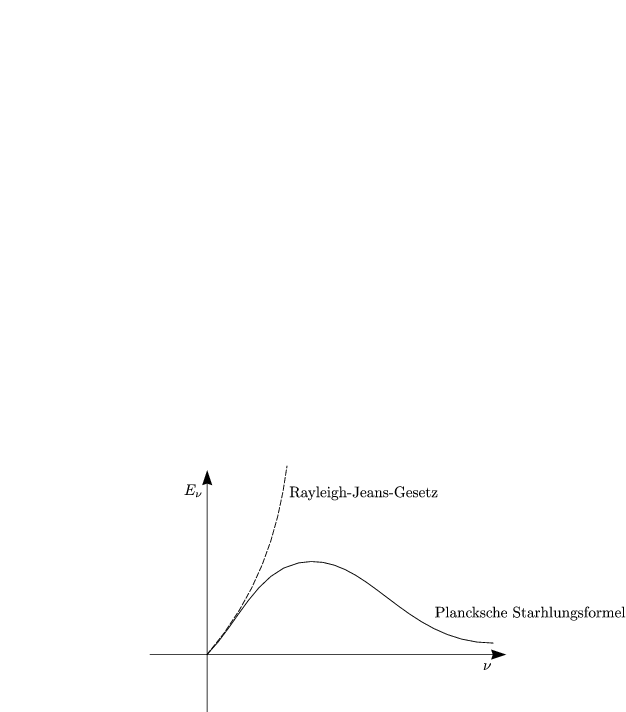
  Die Lage des Intensitätsmaximums genügt dem Wienschen Verschiebungsgesetz:

  

2.1.2 Spezifische Wärme von Festkörpern

In Physikalische Chemie I hatten wir folgende Beziehung hergeleitet:

2.1.3 Photoelektrischer Effekt

Der photoelektrische Effekt zeigt die Teilchennatur des Lichts (1887: Heinrich Hertz; 1905: Albert Einstein).

Experiment:

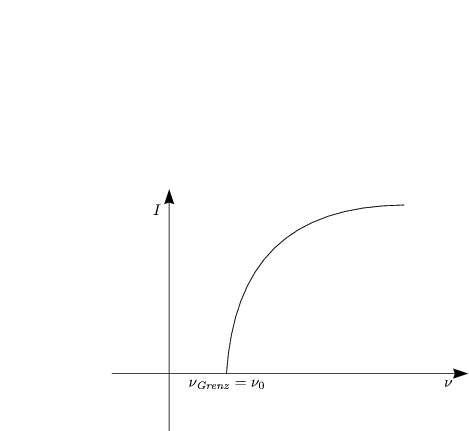
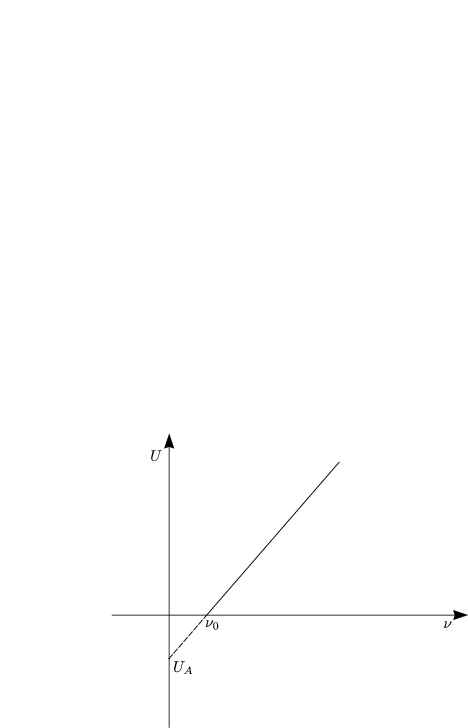
Die Kathode besteht aus Metall wie beispielsweise Cäsium.

1. Strom detektierbar, wenn > ₀
2. Bestimmung der kinetischen Energie der Elektronen durch Anlegen einer Gegenspannung:

   U_A ist ein Schwellenwert; er spiegelt die Austrittsarbeit eines Elektrons aus dem Metall wider.

Beobachtung:

Die Elektronenzahl hängt nur von der Intensität ab, nicht von der Energie. Die quantenmechanische Erklärung ist, daß die Strahlungsenergie nur in diskreten Beiträgen absorbiert wird.

2.1.4 Der Comptoneffekt

Falls Lichtquanten (mit E = h) sich wie Teilchen verhalten, sollten sie auch Impuls haben. Relativistisch betrachtet gilt m = = . Mit p = mc folgt p = . Den experimentelle Beweis hat COMPTON im Jahre 1922 erbracht bei der Streuung von Röntgenstrahlen an Graphit.

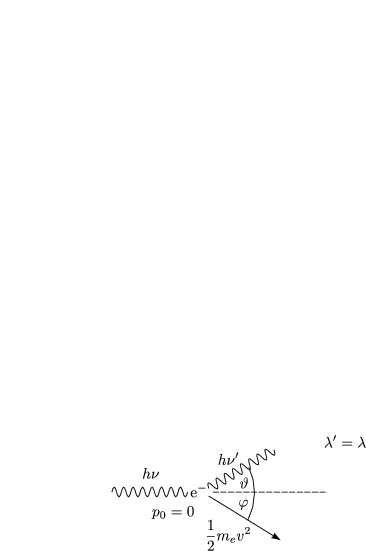
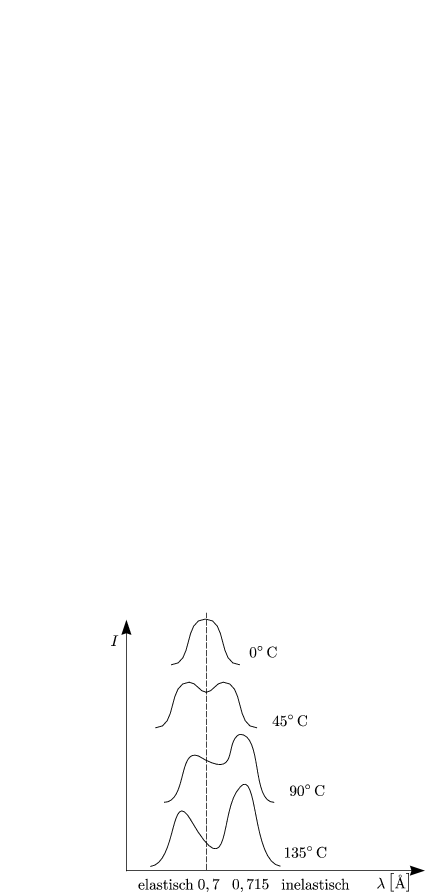
Die klassische Erwartung ist, daß es einen viel größeren -Verschiebungsbereich gibt, welcher anhängig von h ist (Originalexperiment: K-Strahlung von Molybdän auf Graphit).

• Energieerhaltung:

• Impulserhaltung (in x-Richtung):

• Impulserhaltung (in y-Richtung):

Aus diesen drei Gleichungen ergibt sich:

Daraus folgt, daß Photonen korpuskular sind.