Wir erinnern uns, daß das Übergangsdipolmonent gegeben ist durch ![]() fi = <vf|
fi = <vf|![]() |vi>
und suchen nun die allgemeine Auswahlregel (für zweiatomiges Molekül)
mit f(R) und R = Re. Dazu entwickeln wir
|vi>
und suchen nun die allgemeine Auswahlregel (für zweiatomiges Molekül)
mit f(R) und R = Re. Dazu entwickeln wir ![]() fi in eine Taylor-Reihe um
Re:
fi in eine Taylor-Reihe um
Re:

Daraus ergibt sich die allgemeine Auswahlregel ![]() R=Re
R=Re![]() 0.
0.

Das Dipolmoment muß sich bei Änderung des Kernabstands auch ändern.
Beispielsweise haben heteromolekulare zweiatomige Moleküle im allgemeinen ein
Dipolmoment, das sich mit dem Abstand ändert. Beispielsweise ist HCl IR-aktiv. Für
homomolekulare zweiatomige Moleküle gilt ![]() = 0 für alle Bindungslängen, womit
diese IR-inaktiv sind.
= 0 für alle Bindungslängen, womit
diese IR-inaktiv sind.
Wir berücksichtigen die hermetischen Polynome in der Wellenfunktion:
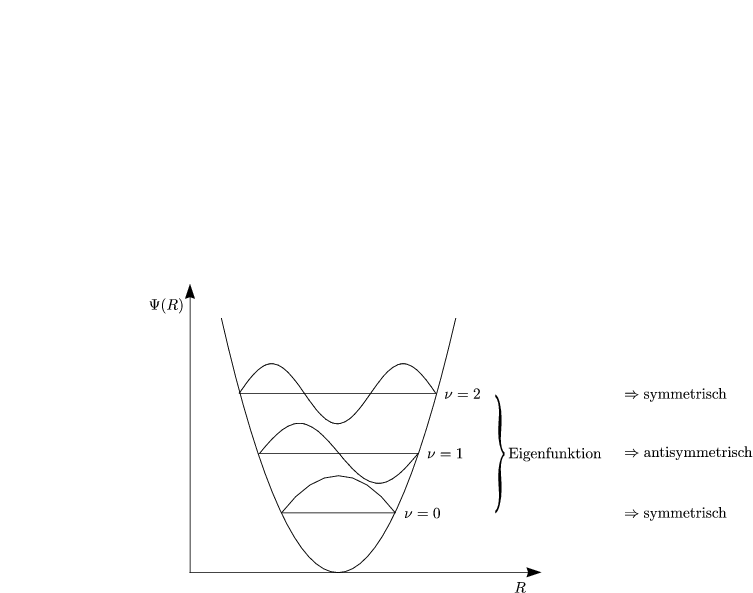
Hier gilt <vf|![]() |vi>
|vi>![]() 0 für
0 für ![]() v = ±1.
v = ±1.
Es ist eine analoge Betrachtung wie für harmonischen Oszillator möglich:
Betrachten wir als Beispiel HCl:
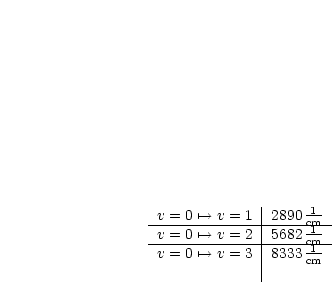
Betrachten wir die Potentialkurven eines zweiatomigen Moleküls (harmonisch und anharmonisch):
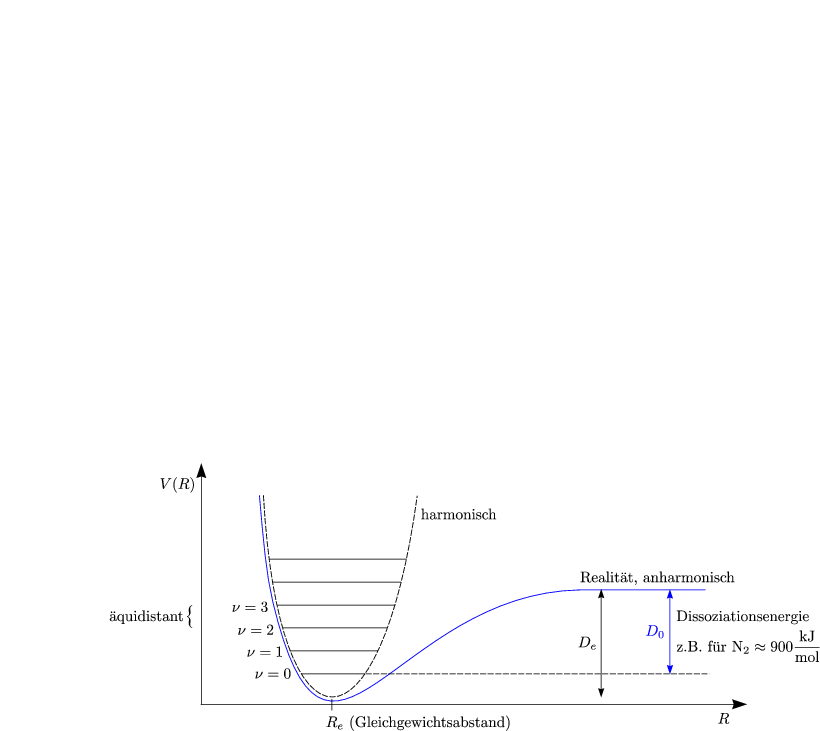
Um das Verhalten von V (R) zu untersuchen, führen wir eine Taylor-Reihenentwicklung von Re durch:

Wir brechen nach der zweiten Ableitung ab und erhalten die harmonische Näherung
mit der Kraftkonstanten k = ![]() , welche eine Charakteristik für die
„Krümmung des Potentials“ ist. Wir setzen V (R) in die Schrödinger-Gleichung ein
und erhalten:
, welche eine Charakteristik für die
„Krümmung des Potentials“ ist. Wir setzen V (R) in die Schrödinger-Gleichung ein
und erhalten:

Die Näherung ist in der Regel ab v = 3 schlecht. Außerdem wird keine Dissoziation berücksichtigt. Besser ist das anharmonische Potential. Dies erhält man, indem man die höheren Ableitungen in der Taylor-Reihe berücksichtigt.
Hieraus ergibt sich:

Wobei xe die Anharmonizitätskonstante darstellt.
Die Boltzmann-Verteilung ergibt die Besetzungsdichten für Schwingungsniveaus.
Das heißt, etwa 1% (meistens weniger) befinden sich im Zustand v = 1, demnach
„Heiße Banden“ (hot bands) für v = 1![]() v = 2. Bei hohen Temperaturen (
v = 2. Bei hohen Temperaturen (![]() 1000 K)
sind damit Übergänge verschoben zu kleinen Wellenzahlen. Betrachten wir außerdem
die Obertöne:
1000 K)
sind damit Übergänge verschoben zu kleinen Wellenzahlen. Betrachten wir außerdem
die Obertöne:
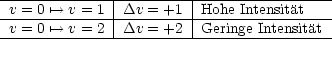
Schnell schwächer werdende bis vernachlässigbare Intensitäten
Es findet eine Polarisationsänderung statt während das Molekül schwingt. Beispielsweise ist H2 IR-inaktiv, aber Raman-aktiv.
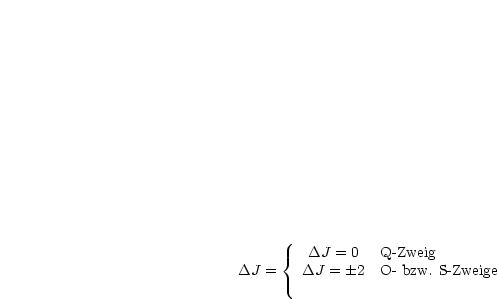
N ist die Anzahl der Atome im Molekül.
Dies sind linear voneinander unabhängige synchrone Bewegungen, welche selektiv (resonant) angeregt werden können.
![]()
Infrarot-inaktiv aber Raman-aktiv.
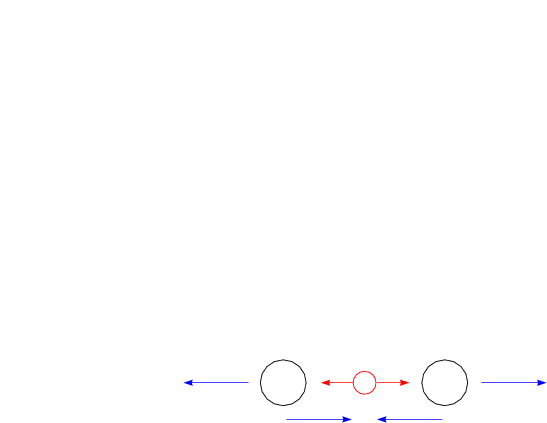
Infrarot-aktiv aber Raman-inaktiv

Infrarot-aktiv aber Raman-inaktiv
O-Atome tauchen in Tafelebene ein. Die ![]() 2-Mode ist entartet.
2-Mode ist entartet.
Klassifizierung von Normalmoden durch Symmetrie des Moleküls (![]() Charaktertafeln)
Charaktertafeln)
Gleichzeitige Anregung von Rotation bei Aufnahme von Schwingungsspektren
möglich, da h![]() vib ~ (100 - 1000)h
vib ~ (100 - 1000)h![]() rot (aber auch
rot (aber auch ![]() J = 0)
J = 0)
Diese sind ![]() v = ±1 (+Absorption) und
v = ±1 (+Absorption) und ![]() J = ±1.
J = ±1.
Betrachten wir das vereinfachte Rotations-Schwingungsenergieschema und das daraus resultierendes Spektrum für ein zweiatomiges Molekül:
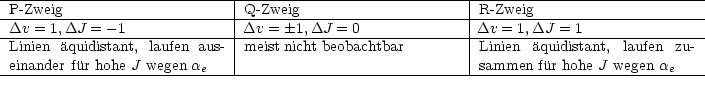
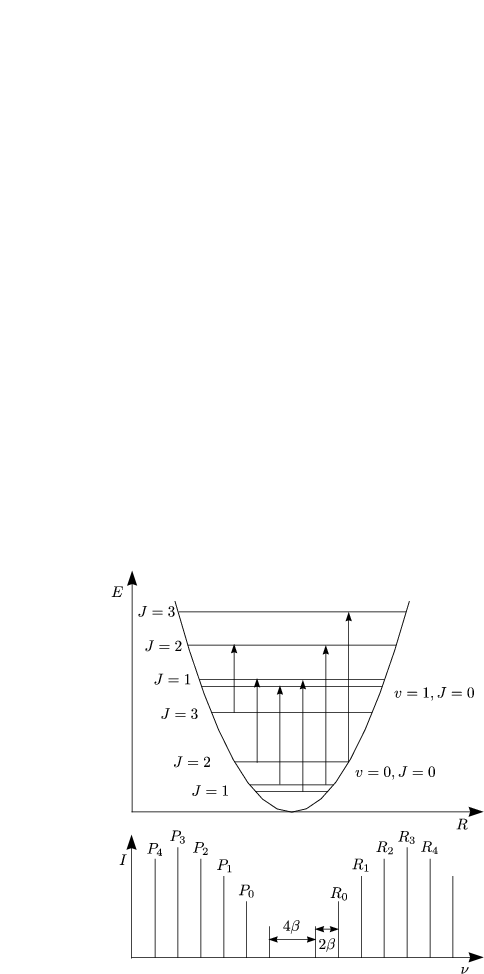
Damit wird die Rotationsfeinstruktur aufgehoben.
Betrachten wir als Beispiel wieder H2O.
Schauen wir uns also das Spektrum von Wasser an:

Man versucht, die Empfindlichkeit von IR-Messungen zu erhöhen. Betrachten wir hierzu den interferometrischen Aufbau. Es handelt sich prinzipiell um ein Michelson-Interferometer:
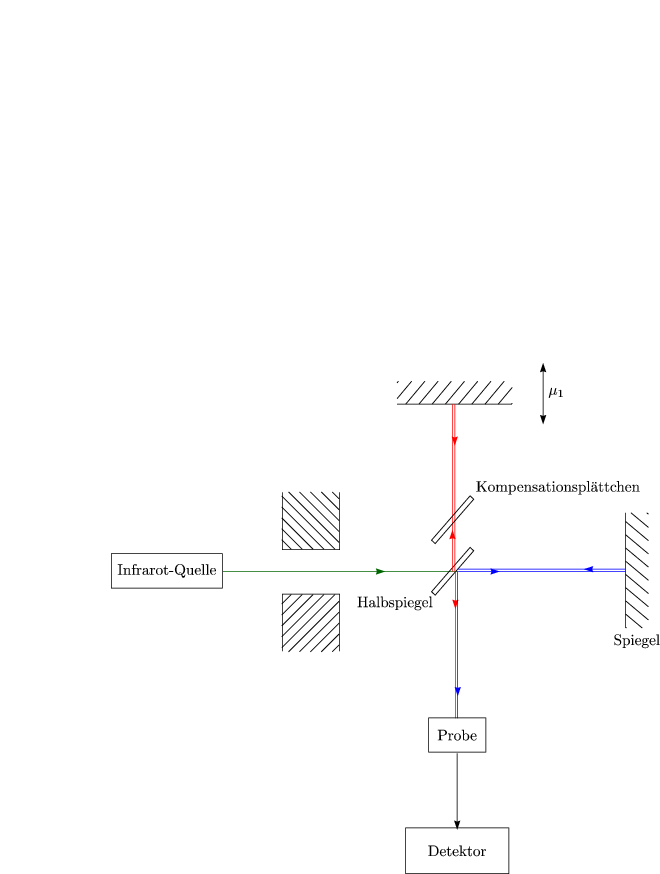
Gemessen wird die Zeit oder der Weg. Durch Fouriertransformation erhält man dann das Spektrum. Mit monochromatischem Licht folgt:
![]() ist hierbei der Gangunterschied der beiden Strahlen auf Detektor. Mit
polychromatischen Licht erhält man:
ist hierbei der Gangunterschied der beiden Strahlen auf Detektor. Mit
polychromatischen Licht erhält man:
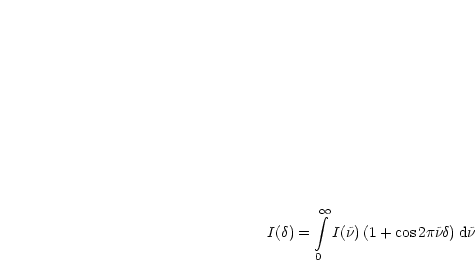
Die Fourier-Transformation wird durch Standard-Computerprogramme
hauptsächlich durch den Algorithmus der Fast Fourier Transformation (FFT)
durchgeführt. Es ergibt sich die Auflösung ![]()
![]() ~
~![]() , beispielsweise gilt für 5cm
, beispielsweise gilt für 5cm
![]()
![]() ~ 0,1
~ 0,1![]() .
.
Allgemein erhalten elektronische Spektren elektronische Schwingungs- und Rotationsbeiträge. Es sind damit einfache analytische Ausdrücke für elektronische Energieniveaus nicht mehr möglich.
Beziehungsweise Entkopplung der Wellenfunktionen:
Die Energie nimmt zur Rotationsenergie hin ab.
Man führt eine Trennung von elektronischen- und Kernbeiträgen durch. Diese besitzt folgende Anwendungen: