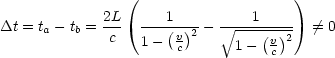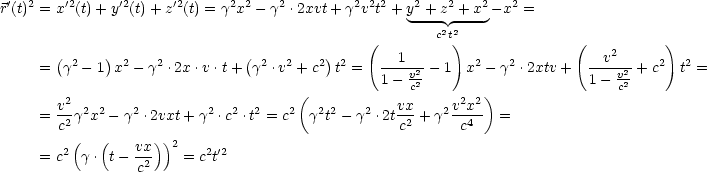- OLAF RÖMER 1675:
Messung des Zeitpunktes der Verdeckung des Mondes Jupiters:
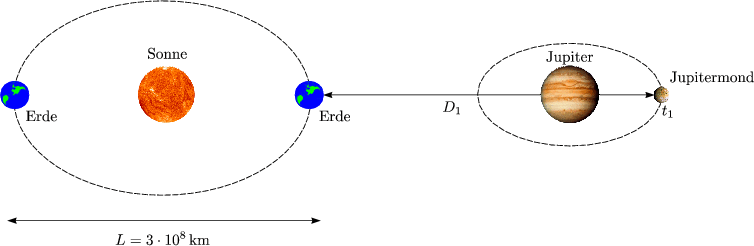
Ein halbes Jahr später:
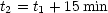
Damit folgt für die Lichtgeschwindigkeit:
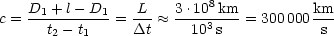
Römer hatte c = 200000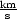 berechnet!
berechnet!
- FIZEAU (1849):
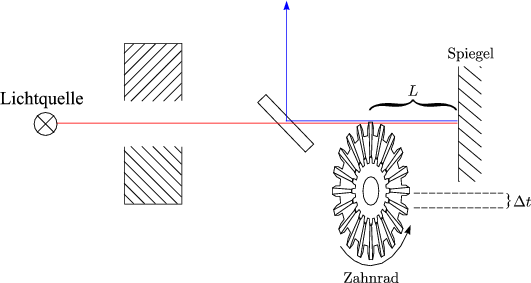
Licht wird vom Zahnrad absorbiert, wenn 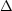 t =
t = 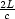 . Damit errechnet sich
c folgendermaßen:
. Damit errechnet sich
c folgendermaßen:
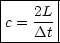
Heute kann man c sehr genau bestimmen:
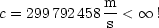
- Beweis, daß Lichtgeschwindigkeit c unabhängig vom Bezugssystem:
Betrachten wir hierzu das Experiment von MICHELSON, MORLEY (1887)
(Idee von MAXWELL):
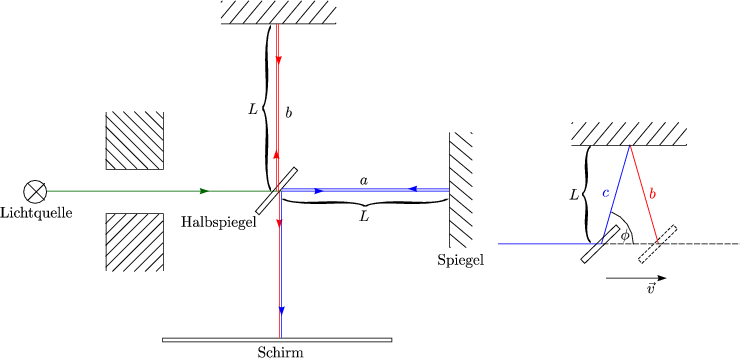
Das System befindet sich auf der Erde, d.h. v = 30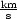 . Die Laufzeit
zwischen Spiegel und Halbspiegel beträgt:
. Die Laufzeit
zwischen Spiegel und Halbspiegel beträgt:
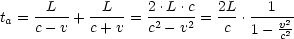
Die Laufzeit von b.) beträgt:
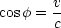
Wir erhalten außerdem für die Laufstrecke s:
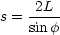
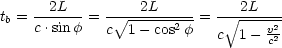
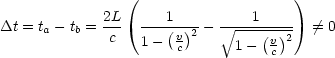
Dabei wird folgende Beobachtung gemacht:
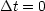
Allgemein gilt:
- Die Zeitdilatation
Wir betrachten folgende Uhr:
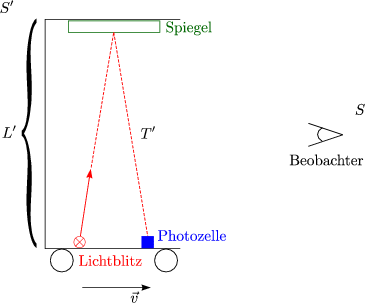
Wenn der Lichtpuls auf die Photozelle auftrifft, wird ein neuer Puls
ausgesendet: Die Periodendauer ist T' = 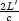 . Für den Beobachter ergibt
sich T = t3 - t1.
. Für den Beobachter ergibt
sich T = t3 - t1.
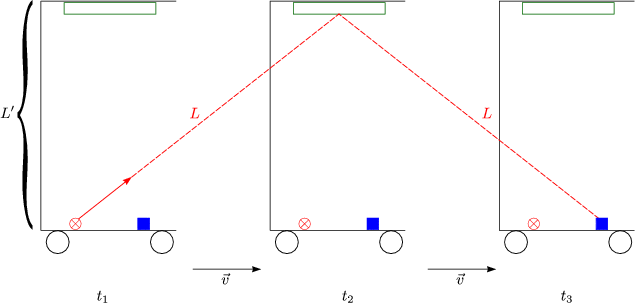
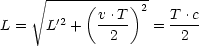
Hieraus ergibt sich:
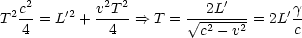
Mit L' = 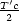 folgt T =
folgt T = 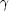 . T'; man spricht von der Zeitdilatation.
. T'; man spricht von der Zeitdilatation.
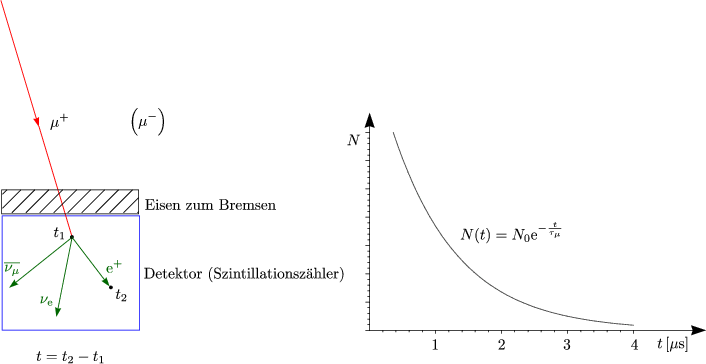
Anwendung: Kosmische Höhenstrahlung
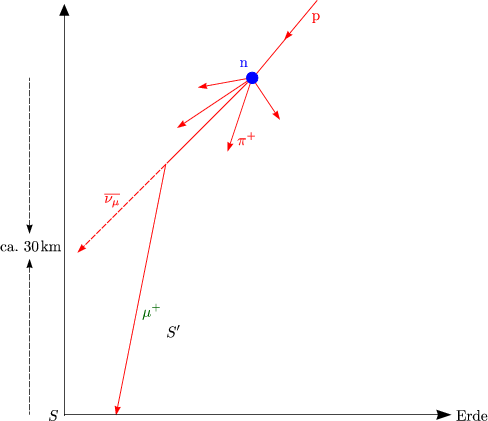
Wir betrachten den Zerfall von Myonen (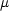 ). Die Lebensdauer eines Myons
beträgt
). Die Lebensdauer eines Myons
beträgt 
 ' = 2,2 . 10-6 s. Für die zurückgelegte Lichtstrecke ergibt sich
L' =
' = 2,2 . 10-6 s. Für die zurückgelegte Lichtstrecke ergibt sich
L' = 
 .c
.c  660m. Im System S (Ruhesystem der Erde) gilt jedoch aufgrund
der Zeitdilatation
660m. Im System S (Ruhesystem der Erde) gilt jedoch aufgrund
der Zeitdilatation 
 =
= 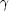 .
. '
' . In unserem Falle gilt
. In unserem Falle gilt 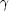 = 50 (v . 0,9998 .c) und
damit im System S:
= 50 (v . 0,9998 .c) und
damit im System S:
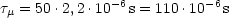
Myonen legen im System S also folgende Wegstrecke zurück:
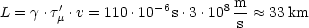
Einschub: Bestimmung von 

- Längenkontraktion
Betrachten wir als Beispiel einen Stab der Länge LS.
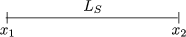
Im System S' gilt:
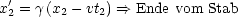
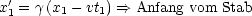
Die Längenmessung wird durchgeführt, indem man beide Enden zur gleichen
Zeit t2 = t1 mißt. Hieraus ergibt sich:
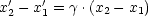
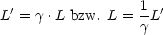
Man spricht von der Längenkontraktion.
Beispiel:
Geschwindigkeit eines Raumschiffes, das Galaxis innerhalb von 30 Jahren
durchlaufen soll.
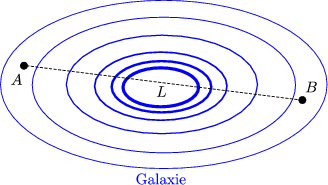
- Rakete: Ruhesystem S
- Galaxis: Bewegtes System S'
Damit erhalten wir L' = 6 . 1020 m und TR = 30 . 3,16 . 107 s  109 s. Für die
Wegstrecke L im System des Raumschiffs gilt L =
109 s. Für die
Wegstrecke L im System des Raumschiffs gilt L = 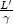 . Mit
. Mit
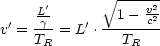
erhalten wir dann:
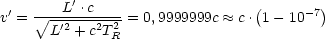
Auf der Erde gesehen ergibt sich eine Zeit von:
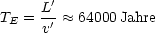
- Addition von Geschwindigkeiten
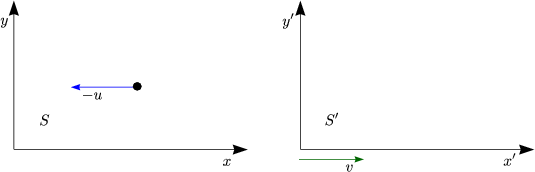
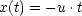
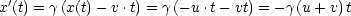
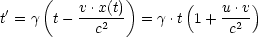
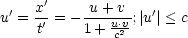
Beispiel:
Es sei u = 0,8c und v = 0,8c. Damit folgt:
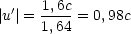
Es gibt somit keine Überlichtgeschwindigkeiten!

![]() berechnet!
berechnet!

![]() t =
t = ![]() . Damit errechnet sich
c folgendermaßen:
. Damit errechnet sich
c folgendermaßen:

![]() . Die Laufzeit
zwischen Spiegel und Halbspiegel beträgt:
. Die Laufzeit
zwischen Spiegel und Halbspiegel beträgt: