[prev] [prev-tail] [tail] [up]

Kapitel 13
Das Plancksche Strahlungsgesetz

Im Photonen-Bild ist Licht in einem Körper nichts anderes als ein ideales Gas aus Photonen. Da die Photonenenergie gequantelt ist (siehe Quantenoptik), handelt es sich um ein Quantengas. In Erinnerung an die Quantenoptik betrachten wir einen von innen verspiegelten Würfel der Kantenlänge L (Hohlraum), d.h. es gibt die Randbedingungen E(Oberfläche) = o. Dies führt dann einfach zu stehenden Wellen.

PIC

|-----------------------------------| E = E0 sin(kxx)sin(kyy)sin(kzz).sin(wt) | ------------------------------------

|---------| | (k ) | | kx | k = ky | | z | -----------

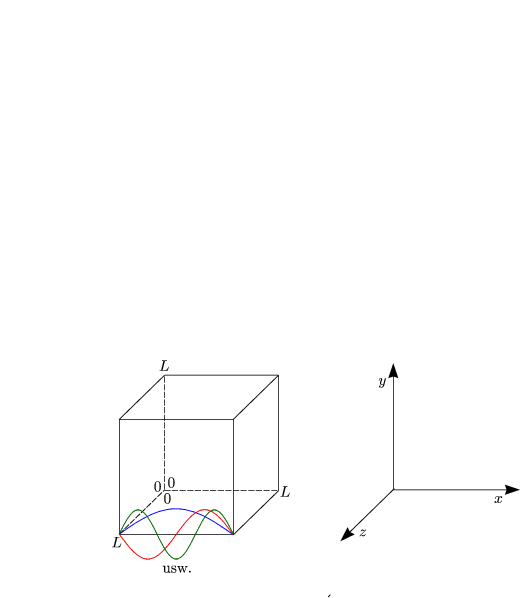
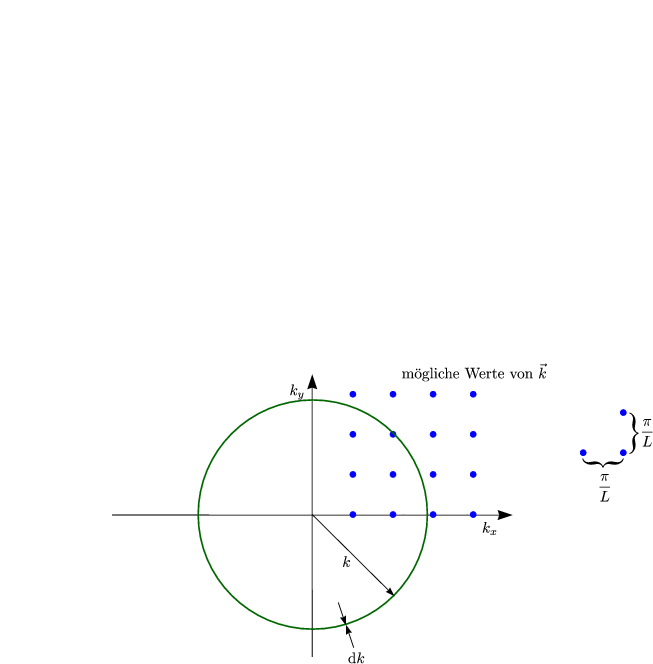
Folgenden Werte von k sind unter Erfüllung der Randbedingungen möglich:

p kx = mx L-mit mx (- N

ky = my p-mit my (- N L

p- kz = mz L mit mz (- N

Beispielsweise führt kx = -p- L führt zu E'-->-E, was somit keine linear unabhängige Lösung dar.

PIC

Zu jedem k gibt es zwei linear unabhängige Polarisationsvektoren E0. Der Index s bezeichne diese Möglichkeiten. Die Indizes k und s numerieren alle möglichen linear unabhängigen Lösungen für E durch. Sie heißen auch Quantenzahlen. Jede Lösung hat eine Frequenz f mit 2pf = wk,s. Die zugehörige Energie (Photonenenergie) ist quantisiert, d.h. es gilt:

E = n.h .f = nk,s .h-wk,s mit nk,s (- N0 2p

Da die Energie nicht von der Polarisation abhängt, können wir den Index s zuerst streichen:

E = n .h--w k 2p k

|-------| |------------| | h | -E-=-nk .h-.wk-mit|h := 2p-| --------

|----------------------------------------------------------------------------------------| | | |Was ist die innere Energie U dieses Quantengases aus Photonen? /\ = Plancksches Strahlungsgesetz | | | -----------------------------------------------------------------------------------------

Die innere Energie ergibt sich jetzt einfach alls Summe aller Zustände, die das Quantengas einnehmen kann:

< > sum sum sum U = <E> = Ek = <Ek> = <nk>hwk k,s k,s k,s

Zunächst stellt sich die Frage, wie sich der Erwartungswert <nk> berechnet.


 13.1 Der Bose-(Planck)-Faktor
 13.2 Die Zustandsdichte

[prev] [prev-tail] [front] [up]