13.2 Die Zustandsdichte

[prev] [prev-tail] [tail] [up]

13.2 Die Zustandsdichte

Unser Vorgehen ist nun folgendes:

1.Schritt:
Wir wollen die Summe in ein Integral überführen.
$sum integral '--> d3k k$
2.Schritt:
Das dreidimensionale Integral über den -Raum soll zu einem eindimensionalen Integral über die Energie werden:
$integral integral d3k '--> dE$
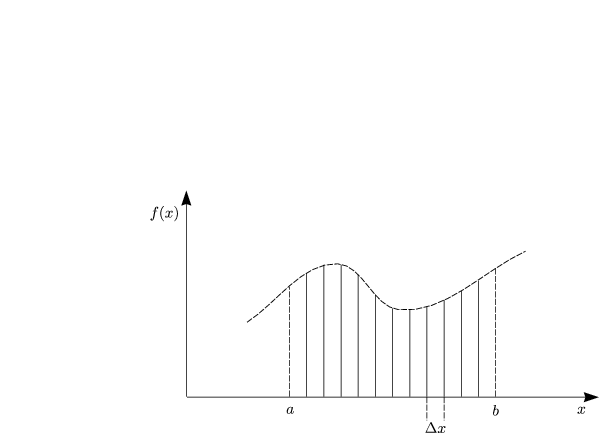
Zu Erinnerung notieren wir uns nochmals die mathematische Definition des Integrals:
$|-b------------------------| | integral sum | | f(x)dx = Dlxim'-->0 Dxf (xi)| -a---------------i----------$
x soll beliebig klein sein und die x_i beliebig dicht liegen.

Analog gilt also:
$Dx /\ = p L$

$integral ( )3 integral sum in 3=D--1-- d3k = 1 .--1-- d3k (p-)3 2 (p)3 k L kx,ky,kz>0 L$
Da es zwei Polarisationsrichtungen gibt, gilt:
$integral sum '--> 2.(-1)- d3k 2pL 3 k,s$
Dies ist gerechtfertigt, weil beispielsweise für sichtbares Licht gilt:
$2p 2p k = --- ~~ ----, Gr¨oße des K¨orpers L ~~ 1cm c 1mm$

$k = 104 .2p L$
Dann hat man also sehr feine Schritte.
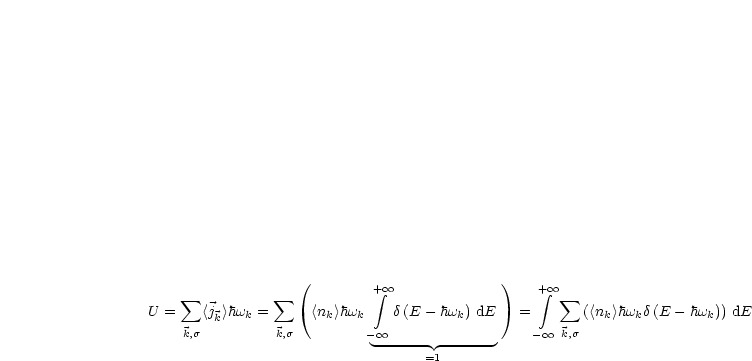
$sum sum ( + integral oo ) + integral o o sum U = <j >hwk = <nk>hwk d(E - hwk) dE = (<nk>hwkd (E - hwk)) dE k,s k k,s - oo - oo k,s ------- ------- =1$
Aufgrund der -Funktion tragen nur die Werte von in der Summe etwa bei mit E = _k.
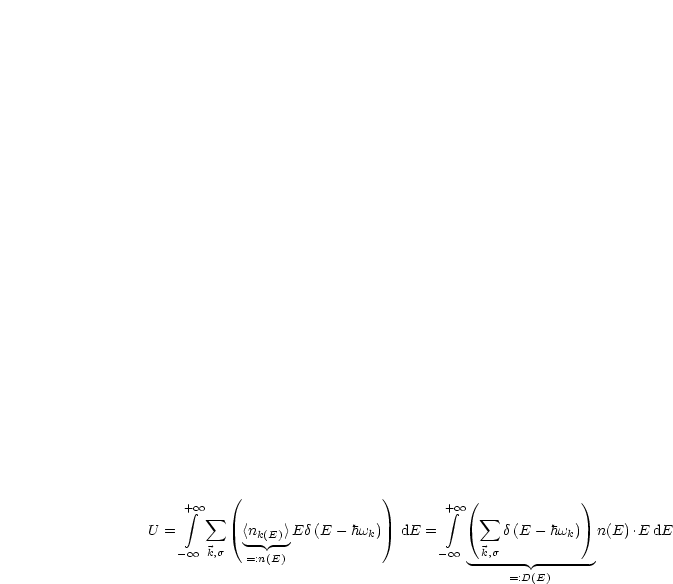
$( ) + integral oo sum + integral oo (s um ) U = <nk(E)>Ed(E - hwk) dE = d(E - hwk) n(E).E dE - oo k,s -- -- - oo k,s =:n(E) ------- ------- =:D(E)$
Somit folgt als Zwischenergebnis:
$|-----------------------|| | + integral o o || |U = D(E) .n(E) .E dE || | - oo || --------------------------$
D(E) ist die sogenannte Zustandsdichte; bei n(E) handelt es sich um den schon definierten Bose-Faktor:
$n(E) = ---(-1-)----- exp kET- - 1 B$
Wir müssen nun einfach den Ausdruck ausknorzen:
$sum D(E) = d(E -hwk) k,s$
Die anschauliche Bedeutung ist ganz einfach. Es handelt sich um die Zahl der Zustände (Moden, stehende Wellen), deren Energien im Intervall liegen. Mathematisch gilt mit _k = ^. c₀ ^. k:
$sum D(E) = d(E -hwk) k,s$
Wir schreiben dies um in ein dreidimensionales Integral über :
$integral --1-- 3 D(E) = 2(2p)3 d(E - hwk)d k L$
Hier drängen sich dann Kugelkoordinaten auf:
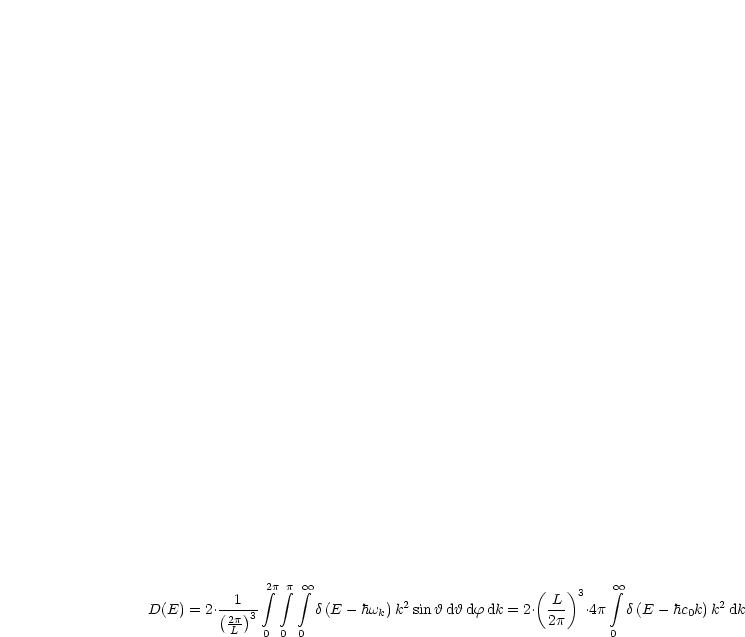
$2 integral p integral p integral oo ( ) integral oo --1-- 2 L--3 2 D(E) = 2.(2p)3 d (E - hwk)k sinh dhdf dk = 2. 2p .4p d (E - hc0k)k dk L 0 0 0 0$
Zur Erinnerung an die -Funktion:
$|-------- sum ----1-----------| d(f(x)) = -'----d(x- xi)| ----------i--|f-(xi)|---------$
x_i sind hierbei die Nullstellen von f(x). Die Nullstelle liegt bei k = . Es gibt aber nur dann Nullstellen, wenn gilt:
$k = |k|> 0 ==> E > 0$
Somit folgt für die Zustandsdichte:
$( ) ( ) L-- 3 -1- E-- 2 D(E) = 2 2p .4p.hc0Q(E) . hc0$

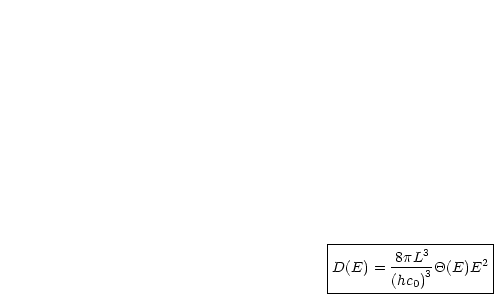
$|--------------------| | 8pL3 | |D(E) = ----3Q(E)E2 | --------(hc0)--------$
Dies ist die Zustandsdichte der Photonen im dreidimensionalen Vakuum. Die Heaviside-Funktion ist definiert durch:
${ 1 f¨ur E > 0 Q(E) := 0 sonst$
Damit folgt für die innere Energie U des Lichtfeldes:
$+ integral oo integral oo sum 8pL3-- -----E3------ U = <nk>hwk = D(E) .n(E).E dE = (hc0)3 exp (-E--)- 1 dE k,s - oo 0 kBT$
Oder mit E = h ^. f gilt für die innere Energie:
$8phL3 oo integral f3 U = ---3-- ---(-hf-)----df c0 0 exp kBT- - 1$
Oder mit U aus der Optik-Vorlesung gilt:
$oo integral U =: V . u(f)df mit V = L3 0$

$|--------------------------| |-------------------3-----|| |u(f,T) = 8p3h---(-f--)----|| | c0 exp hkfBT- - 1|| ----------------------------$
Hier haben wir Somit das Plancksche Strahlungsgesetz erhalten. Weitere Diskussionen (Rayleigh-Jeans, Wiensches Verschiebungsgesetz, Stefan-Boltzmann-Gesetz) siehe Optik-Vorlesung.

[prev] [prev-tail] [front] [up]