13.1 Der Bose-(Planck)-Faktor

Wir erinnern uns an die Bestimmung von Mittelwerten (Erwartungswerten), z.B. den Mittelwert der Augenzahl <A> beim Würfeln. Dieser Mittelwert war gegeben durch:

|------ sum ------| | Ai .pi| |<A> = i sum -----| | i pi | ---------------

Beim Würfel gilt nun:

1 pi = 6; Ai = 1, 2, 3, 4, 5, 6

Damit ergibt sich also für <A>:

<A> = p . sum A = 1.(1+ 2+ 3 + 4+ 5+ 6) = 1.21 = 3,5 i i 6 6

p_i entspricht nun in der Thermodynamik dem Boltzmann-Faktor:

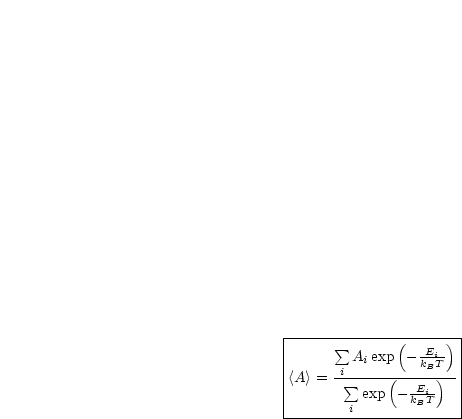
|------ sum ------(--E--)-| | Aiexp - kBiT-- | |<A> = -i sum -----(--E--)--| | exp -kBiT- | ---------i-------------|

Damit folgt dann:

sum oo ( ) n exp - nkhwBkT- <nk> = n= oo 0----(------)- sum exp - nkhwTk n=0 B

Mit der Abkürzung x = exp folgt dann:

oo sum nxn n=0---- <nk> = sum oo n n=0x

Für die geometrische Reihe im Nenner des Bruchs gilt:

sum oo k 1 x = 1---x n=0

Für den Zähler notieren wir uns:

oo sum kxn = ---x--- n=0 (1 - x)2

Also gilt:

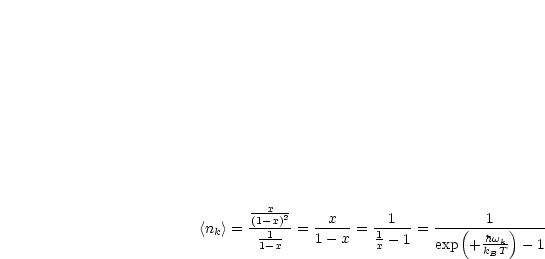
(1x-x)2 x 1 1 <nk> =--1---= 1---x = 1--1-= ----(--hwk-)--- 1-x x exp +kBT - 1

|-------------------| | -----1-------| <nk> = exp (hwk) - 1 | -----------kBT-------

Dabei handelt es sich um die Bose-(Planck)-Verteilung oder auch den Bose-(Planck)-Faktor.

Graphisch:

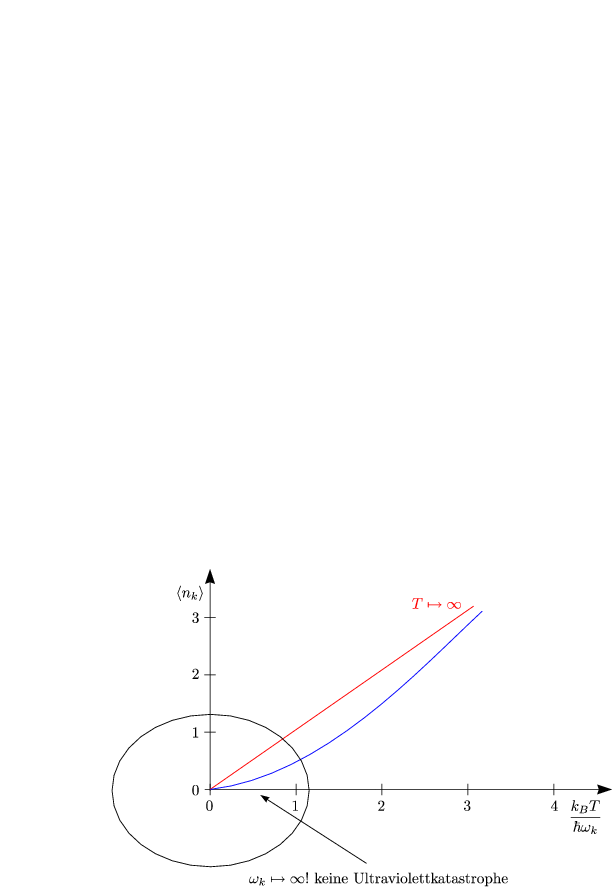
Für T folgt:

<nk> ~~ -----1-----= kBT- 1 + hkwBkT--1 hwk

Somit stehen wir bei:

U = sum <n >hw = ---(-1-)----- k,s k k exp hwk- - 1 kBT

[next] [front] [up]