5.1 Matrixoptik

Will man komplexe Systeme aus Linsen usw. diskutieren, ist oft die Matrixoptik nützlich. Die Idee ist nun folgende: Man charakterisiere einen Strahl an einem Punkt der optischen Achse durch zwei Parameter:

Abstand zur optischen Achse h
Winkel mit optischer Achse

Aus diesen beiden Größen wird ein „Vektor“ gebildet. h und seien hier wieder klein.

h2 = h1 + f1 .L

f2 = f1

( ) ( ) ( ) h2 1 L h1 f2 = 0 1 f1 -M- --- Frei

M_Frei ist 2X2-Matrix. Die Matrix für freie Propagation über die Strecke L ist:

|--------(-----)-| | 1 L | |MFrei = 0 1 | -----------------|

Matrix für eine dünne Linse mit Brennweite f:

h1 = h2

f2 = f1- h1 f

Damit gilt:

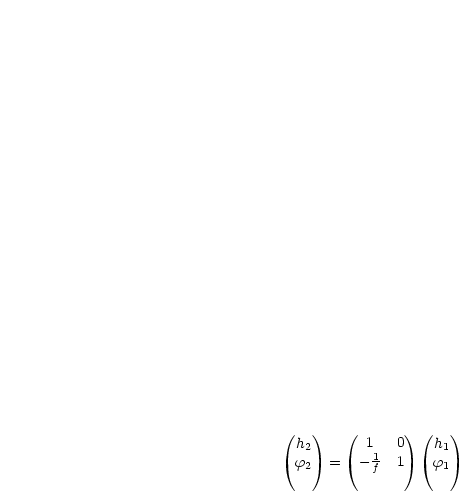
( ) ( 1 0) ( ) h2 - 1 1 h1 f2 = f f1

|---------(------)--| | 11 0 | MKonvex = -f 1 | ---------------------

Für konkave Linsen dito, aber f -f.

Beispiel:

Wir betrachten ein System aus zwei dicht hintereinander liegenden dünnen Linsen mit den Brennweiten f₁ und f₂.

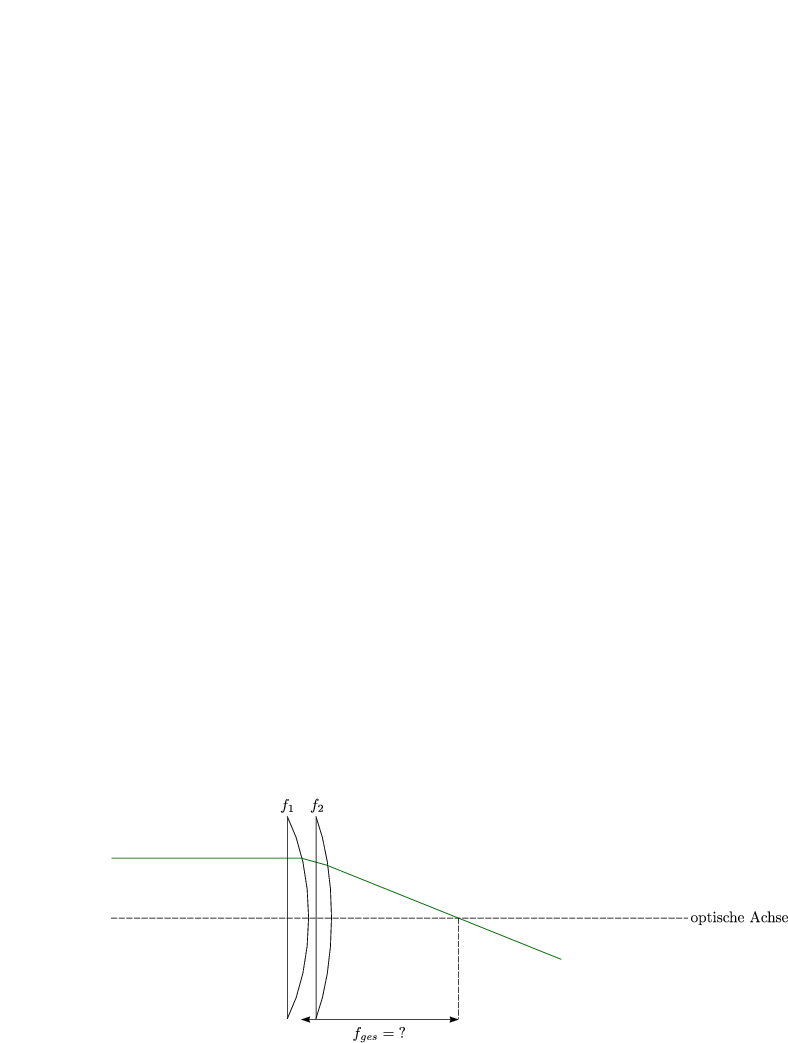
Wir berechnen das Produkt der beiden Matrizen:

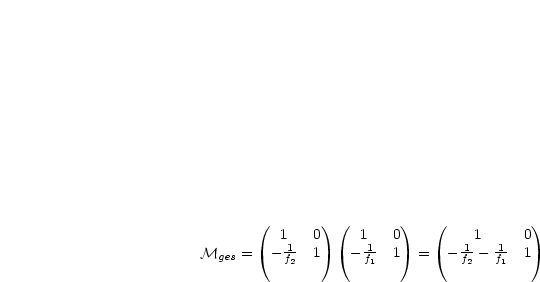
( ) ( ) ( ) 1 0 1 0 1 0 Mges = - 1f2- 1 - 1f1- 1 = - 1f2-- 1f1 1

--1 - 1-= - -1-- f2 f1 fges

Damit gilt also:

|--------------| fg-e1s = f-1 1+ f-21 ----------------

Beispiel (Abbildungen):

Hier müssen drei Matrizen in der richtigen Reihenfolge multipliziert werden:

( ) ( ) ( ) ( ' ' ) 1 a' 1 0 1 a 1 - af- a - aaf-+ a' Mges = 0 1 - 1f 1 0 1 = - 1f - af + 1 --(---- -----)- 11 aa = - f - f + 1

Somit folgt:

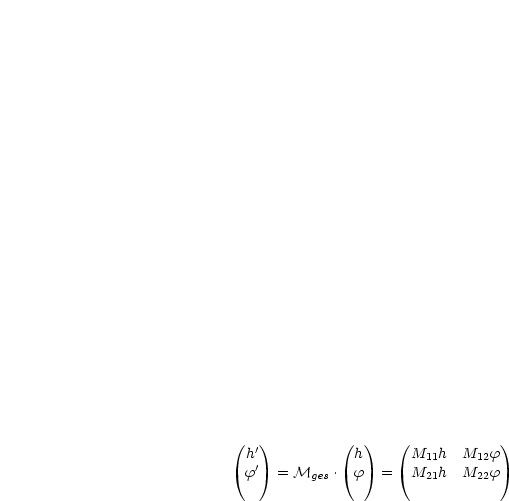
( ) ( ) ( ) h' h M11h M12f f' = Mges . f = M21h M22f

In der Bildebene kreuzen sich die Strahlen mit verschiedenem , d.h. h' hängt nicht von ab. Somit folgt:

M12 = 0

' a- aa- +a'= 0 f

Somit folgt:

|1---1---1-| |--= --+ -'| -f---a---a--

Dies ist die sogenannte Abbildungsgleichung. Die Vergrößerung in der Bildebene ergibt sich nun durch:

a' M11 = 1- f-

Betrachten wir folgendes Zahlenbeispiel. Wir möchten eine zehnfache Vergrößerung, d.h. M₁₁ = -10. Damit resultiert:

a'= 11f

Mit der Abbildungsgleichung ergibt sich dann:

1- 1- 1- 1- -1-- -10- a = f - a'= f - 11f = 11f

|--------| | 11 | |a = 10f | ---------

Beispielsweise folgt mit a < f, daß a' < 0 und die Vergrößerung M₁₁ > 0 ist.

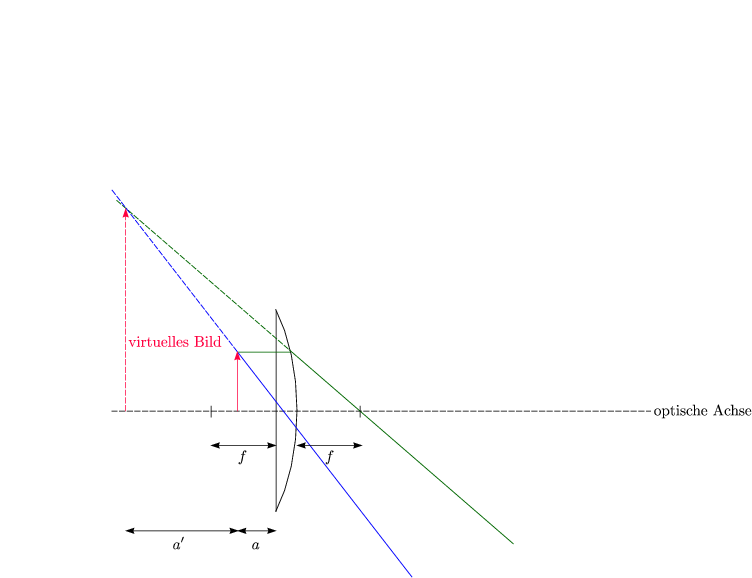
Das virtuelle Bild kann nicht auf einem Schirm aufgefangen werden.

Beispiel (Stabilität optischer Resonatoren):

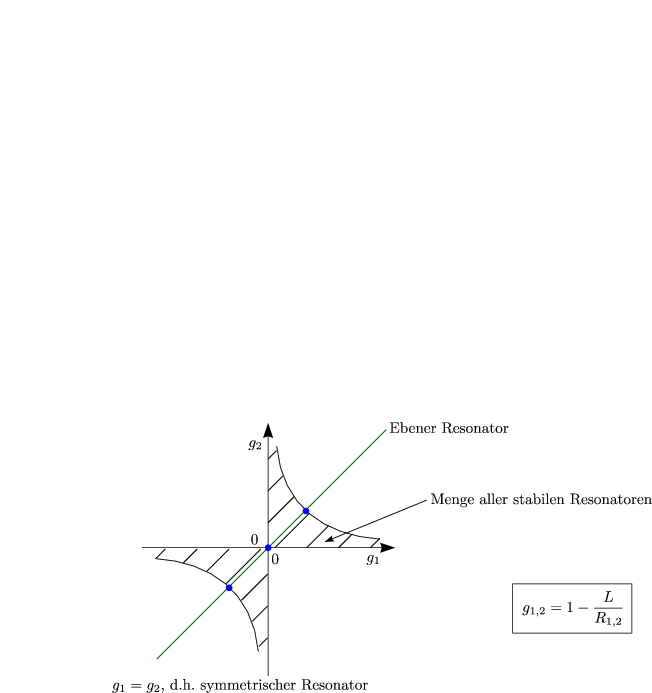
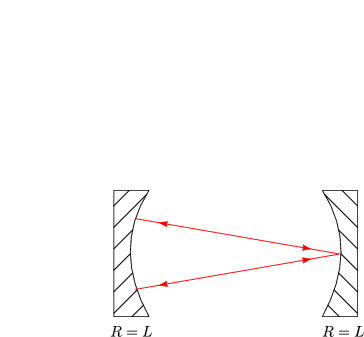
Wir zeichnen einen Resonator prinzipiell:

Fragestellung:

Wie sind R₁, R₂ und L zu wählen, damit der Resonator stabil ist, d.h., daß ein Strahl im Resonator verbleibt? Dazu notieren wir uns zuerst die Matrix eines Spiegels:

|-------------------| | ( 1 0) | M = -1 1 | | Spiegel f | ---------------------

Die Brennweite f des Spiegels hängt dabei folgendermaßen mit seinem Krümmungsradius R zusammen:

|------| |f = R-| -----2-|

Ersatzaufbau:

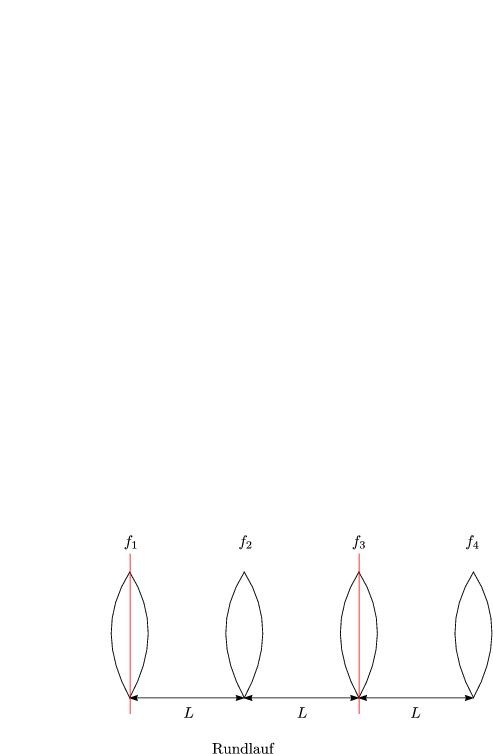
Die halbe Linse hat die Brennweite 2f. Damit folgt die Matrix eines Rundlaufs:

( ) ( ) ( ) ( ) ( ) 1 0 1 L 1 0 1 L 1 0 MRundlauf = - 1f1 1 0 1 - 1f2- 1 0 1 -21f1 1

Damit M eines Matrix im wesentlichen Sinne wird, ersetzen wir den „Vektor“:

( h) ( h ) f '--> f .L /\ = Vektor

Durch Ausmultiplizieren ergibt sich folgendes Zwischenergebnis:

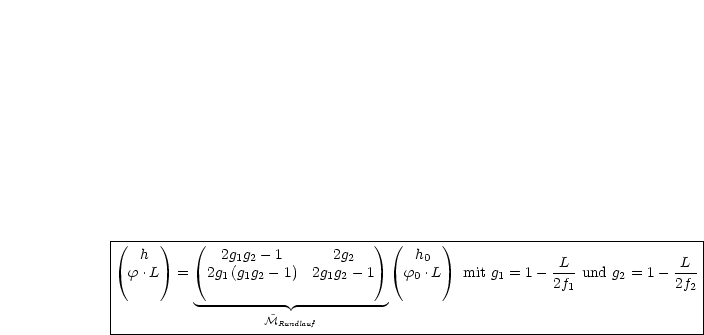
(-----)---(----------------------)-(-----)--------------------------------| | h 2g1g2 -1 2g2 h0 | | f .L = 2g1(g1g2 - 1) 2g1g2- 1 f0 .L mit g1 = 1--L- und g2 = 1--L- | | 2f1 2f2 | | ----------- ----------- | -------------------M~Rundlauf-------------------------------------------------

Suche zunächst Eigenlösungen des Systems, d.h.

M~Rundlaufr0 = cr0

Dieses Eigenwertproblem soll nun gelöst werden:

( ) ~MRundlauf- cM r0 = 0

Die notwendige Bedingung für nichttriviale Lösungen ist nun, daß die Determinante der Matrix _Rundlauf - M gleich Null ist:

det(M~ - cM)= 0 Rundlauf

Nach einigen Rechenschritten folgt:

2 c -2 (2g1g2- 1)c + 1 = 0

Diese quadratische Gleichung wird mit der p-q-Formel gelöst, wobei wir dann folgende Eigenwerte erhalten:

|--------------- V~ -------------| -c =-(2g1g2--1)±--4g1g2(g1g2--1)-

Behauptung:

Resonator ist stabil für 0 < g₁g₂ < 1
Resonator ist instabil für g₁g₂ < 0 oder g₁g₂ > 1

Beweis:

0 < g₁g₂ < 1: $±ih c = e = cosh± isin h$
Denn es gilt:
$cosh = 2g1g2 - 1$
Nun muß gelten:
$sin2h = -4g1g2(g1g2 -1)$
Es gilt ja bekanntlich:
$2 2 2 sin h = 1 - cos h = 1- (2g1g2- 1) = -4g1g2(g1g2- 1)$

Die Eigenwerte sind komplexe Zahlen, die den Betrag 1 haben. Wir stellen einen beliebigen Anfangsvektor ₀ als Linearkombination dar:
$r0 = c+r+ + c- r-$
Nach n Rundläufen ergibt sich folgender Vektor:
$r = c e+inh + c e-inhr n + - -$
Dieser Ausdruck ist beschränkt:
$rn = (c+r+-+ c-r-)cos(nh)+ i(c+r+ - c-r-)sin(n .h) r0$
Infolgedessen haben wir einen stabilen Resonator.
g₁g₂ < 0 oder g₁g₂ > 1:
Wir stellen folgende Behauptung auf:
$c = (2g1g2- 1)± V~ 4g1g2-(g1g2---1)-= ± cosh(h)± sinh(h)$

$+h c1 = e$

$c2 = e-h$
Denn es gilt:
$cosh(h) = 2g1g2 - 1$

$sinh2(h) = 4g1g2(g1g2- 1)$

$sinh2(h) = cosh2(h)- 1 = (2gg -1)2- 1 = 4gg (g g - 1) 1 2 12 1 2$
Nach n Rundläufen ergibt sich :
$+nh -nh rn = c+r+e + c-r-e$
Dieser Ausdruck ist nicht beschränkt. Der Resonator ist somit instabil.

Graphisch:

Ebener Resonator:

g1 = g2 = 1

Konfokaler Resonator:

g1 = g2 = 0

Konzentrischer Resonator:

g1 = g2 = -1

[next] [front] [up]