Kapitel 5
Geometrische Optik

Definition:

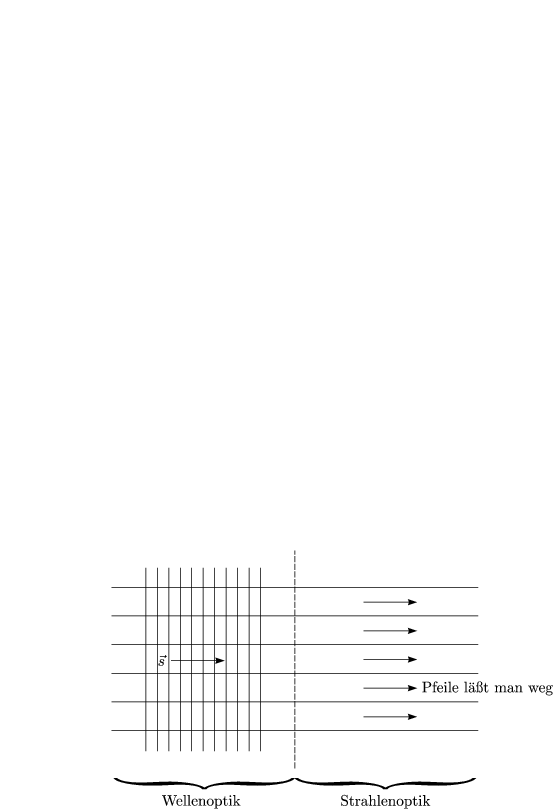
Wir zerlegen eine ebene Welle in Partialwellen. Jede einzelne Partialwelle kann durch ihren Poynting-Vektor (meist ||) charakterisiert werden. Wir vernachlässigen Beugungseffekte! Unter diesen Bedingungen bezeichnen wir die Menge der Vektoren als Lichtstrahlen.

Beispiel:

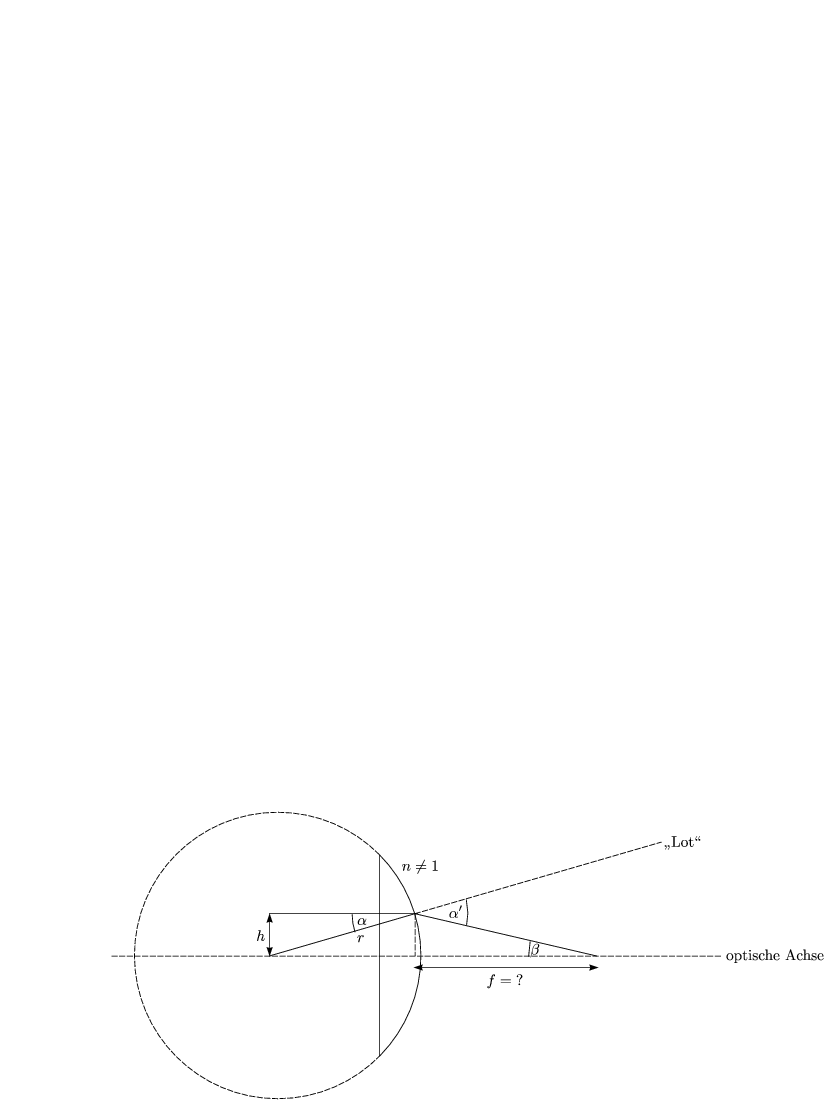
Wir berechnen die Winkelsumme im grünen Dreieck:

Das Snellius Brechungsgesetz angewendet lautet:

Ferner gilt:

Wir verwenden außerdem folgende Näherungen für achsennahe Strahlen (h sei klein) bzw. dünne Linse (r sei groß). Damit können wir den Sinus bzw. den Tangens durch die entsprechenden Argumente approximieren:

Damit ergibt sich die Brennweite der plankonvexen Linse:

f hängt also nicht von h ab:

Man charakterisiert eine Linse durch die Größe ihrer Brechkraft D als Kehrwert der Brennweite f:

Für größere h hängt f doch von h ab. Dies ist die sogenannte sphärische Abberation.

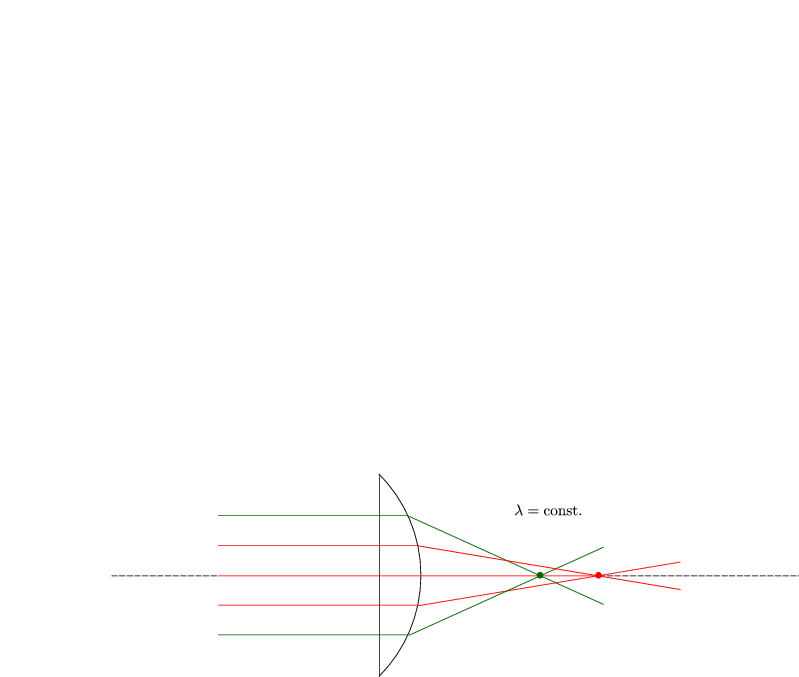
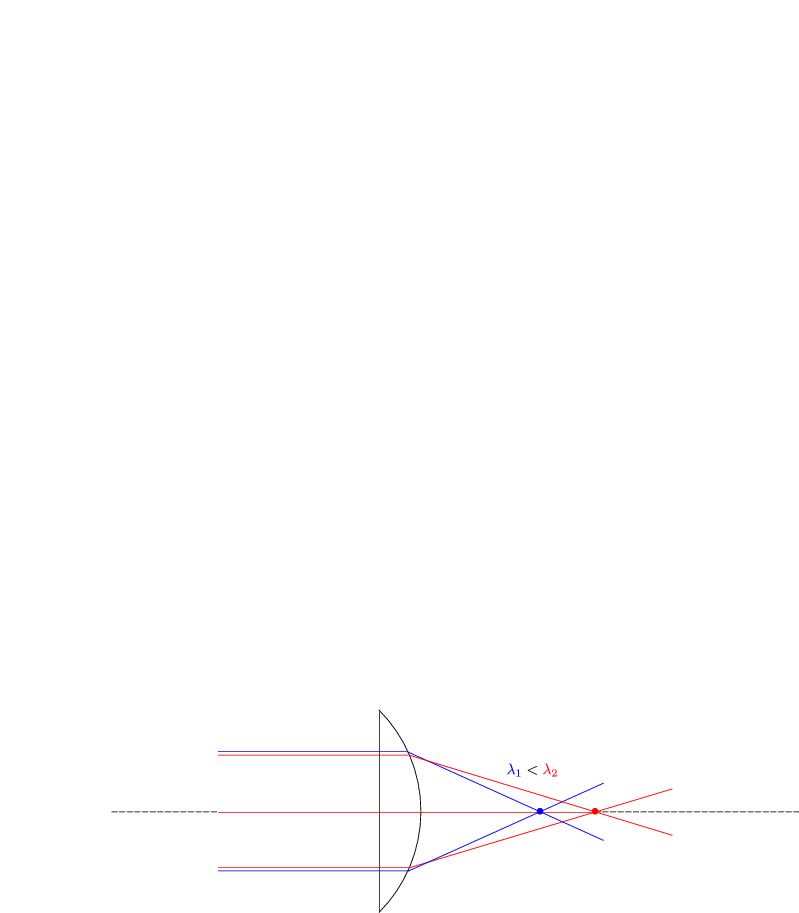
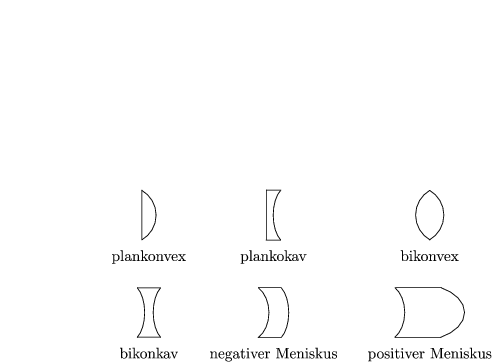
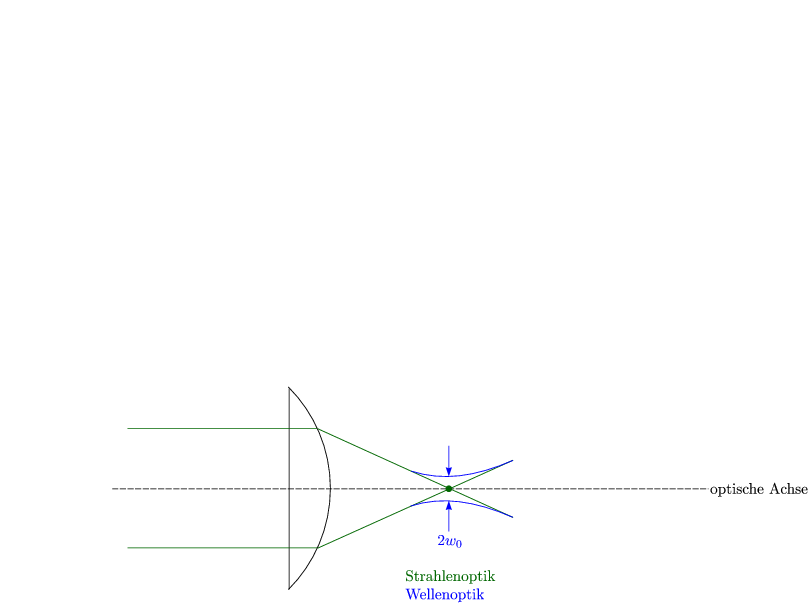
Wie verändert sich das Verhalten in der Wellenoptik? (siehe Kapitel 3.4.3)