5.3 Fermatsches Prinzip

Viele Phänomene der Optik wie beispielsweise Reflexion, Brechung, Linsen, etc. lassen sich - alternativ zu den Maxwell-Gleichungen - auch auf der Basis des Fermatschen Prinzips verstehen.

|----------------------------------------------------------------------------------------|
| |
|Ein Lichtstrahl l¨auft von einem Punkt A zu einem anderen Punkt B auf einem Weg, dessen optische |
|Wegl¨ange minimal ist. |
-----------------------------------------------------------------------------------------

Beispiel:

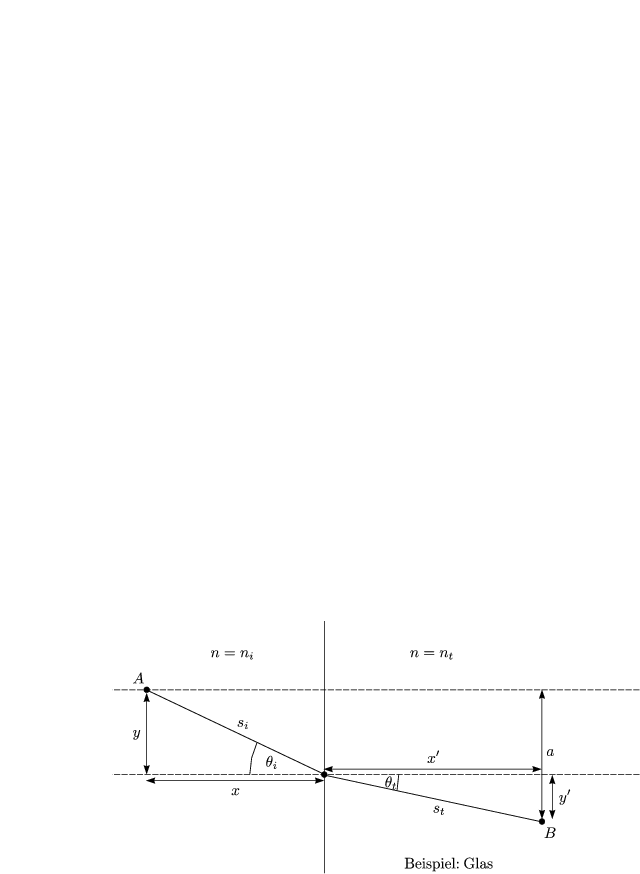
Wir betrachten die Zeit t von A nach B als Funktion von y:

t = si-+ st= -1 (nisi + ntst) ci ct c0 ---- ---- =:Woepgtil¨ascnhgee

Mit dem Satz des Pythagoras folgt:

( V~ -----------) -1 V~ -2---2- '2 2 t = c0 ni x + y + nt x +(a -y)

Wir bestimmen nun das Minimum von t bzw. der optischen Weglänge:

dt-!= 0 dy

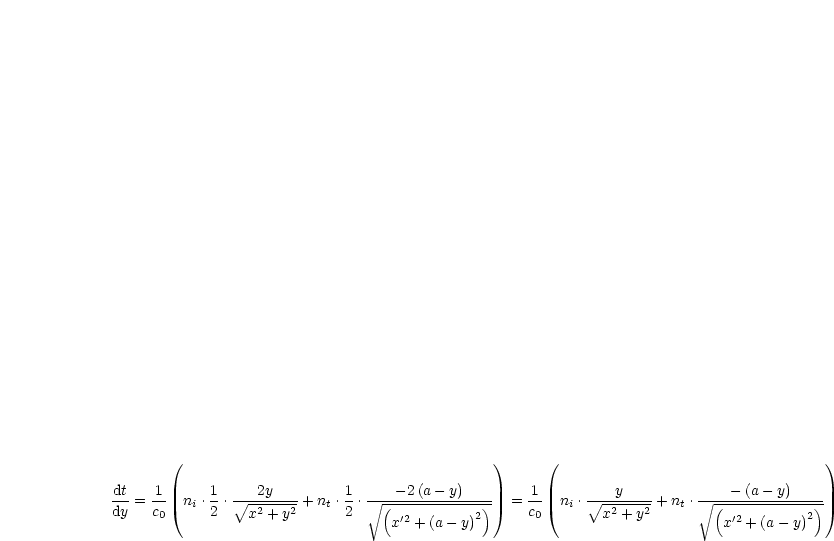
( ) ( ) dt- 1- 1 ---2y---- 1 -----2(a--y)---- -1 ----y---- ------(a--y)---- dy = c0 ni .2 . V~ x2-+-y2-+ nt .2 . V~ (-------2)- = c0 ni . V~ x2-+-y2 + nt . V~ (--------2) x'2 + (a - y) x'2 + (a- y)

Außerdem gilt:

V~ --y---- x2 +y2 = sin hi

V~ --(a--y)----= - sinht x'2 + (a- y)2

Somit folgt dann:

|n-.sin-h-=-n-.sin-h-| --i-----i---t-----t|

Wir erhalten also das Snellius Brechungsgesetz (siehe Kapitel 3.1.2) ohne Verwendung der Maxwellschen Gleichungen! Im Beispiel war die optische Weglänge n_is_i + n_ts_t. Allgemein gilt für die optische Weglänge:

-------------- | integral B | | | so = n(s)ds| -----A--------

Man integriert also vom Startpunkt A bis zum Endpunkt B über den vom Weg s abhängigen Brechungsindex. Das Fermatsche Prinzip lautet nun:

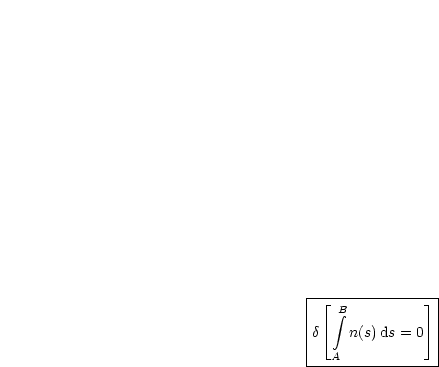
|----------------| | |_ B integral _| | |d |_ n(s)ds = 0 _| | | ---A-------------

bedeutet hierbei die Variation. Dies steht im Zusammenhang mit dem Hamiltonschen Prinzip aus der Mechanik:

| |_ -t--- _| ----| | integral 2 | d |_ L dt _| = 0 | ---t1-----------

L ist hierbei die aus Theorie B bekannte Lagrangefunktion.

[prev] [prev-tail] [front] [up]