8.5 Boltzmann-Verteilung und Maxwell-Verteilung

Auf die Verteilungsfunktion wurde im Kapitel 2.1 nicht eingegangen. Dies wollen wir jetzt nachholen. Es gilt ja:

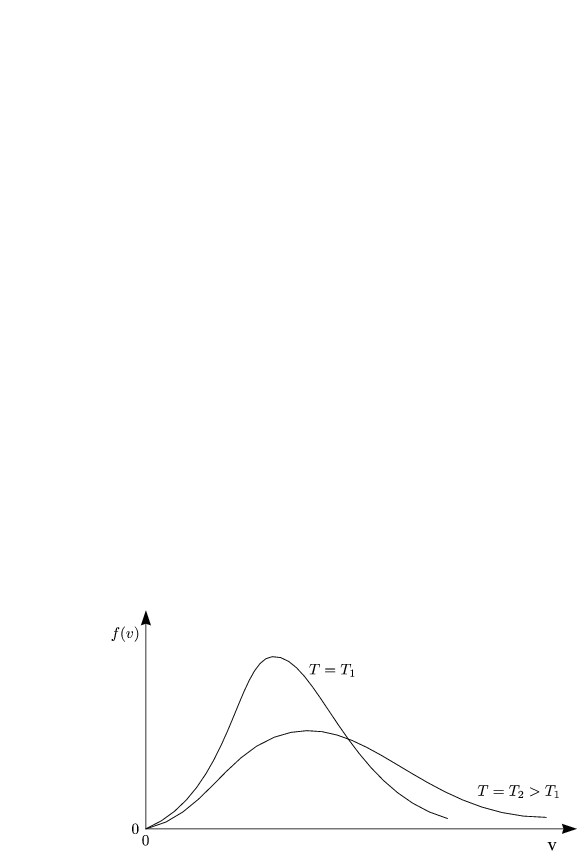
Wir fragen uns nun, wie die Geschwindigkeiten - bzw. die kinetischen Energien - um diesen Mittelwert verteilt sind.

Graphisch:

Beispiel:

Vernachlässigen der potentiellen Energie im Schwerefeld der Erde ergibt:

Wir bilden das Verhältnis:

Beachte: || = v

Definition:

f(v)dv ist die Wahrscheinlichkeit, ein Teilchen mit einer Geschwindigkeit im Intervall v bis v + dv zu finden. Wieviele Geschwindigkeitsvektoren gibt es in diesem Intervall [v,v + dv]?

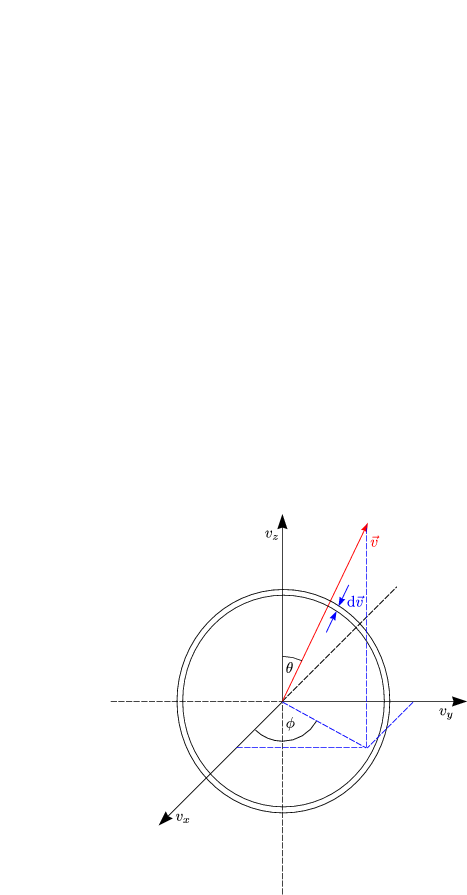
Die Zahl ist proportional zum Volumen der Kugelschale:

Durch Normierung erhält man den Vorfaktor:

Daraus folgt:

Dies ist die sogenannte Maxwellsche Geschwindigkeitsverteilung.