8.6 Entropie

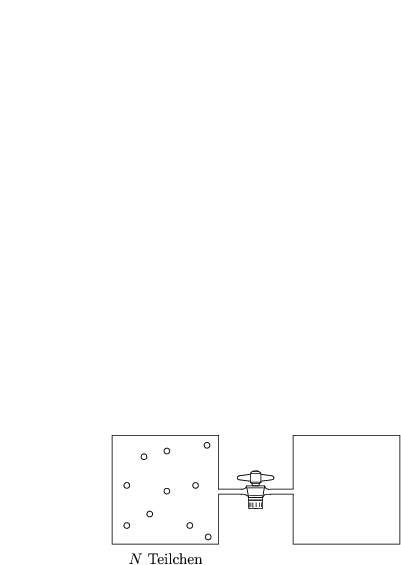
Wir machen ein Gedankenexperiment:

Wir öffnen das Ventil:

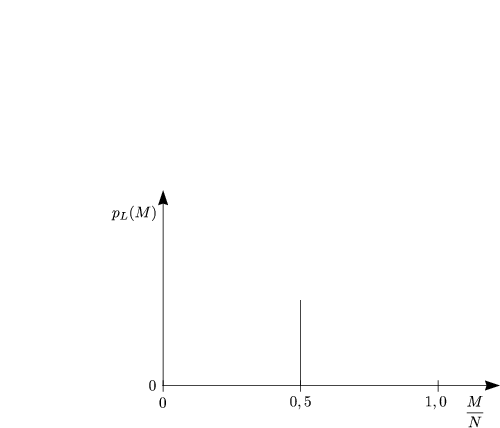
Wir definieren die Wahrscheinlichkeit p_L(M) M Teilchen aus N Teilchen links zu finden. Wir suchen also die Anzahl der Möglichkeiten, im linken Teil M Teilchen aus N auszuwählen (Kombinatorik). Diese berechnet sich nach folgender Formel:

Die Anzahl der Möglichkeiten, N Teilchen auf links/rechts zu verteilen ist 2^N. Dann folgt für die Wahrscheinlichkeit:

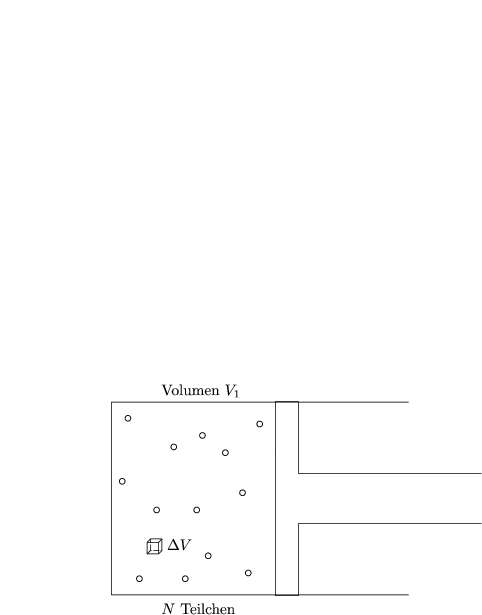
Wir machen ein Gedankenexperiment:

Was ist das Maß für die Gleichverteilung? N Teilchen sind auf m Gefäße verteilt.

Definition:

Beispiel (Gedankenexperiment):

Die Entropie eines Teilchens, das auf m Gefäße verteilt sein kann, lautet:

Mit der speziellen Wahl = und ln(m) = ln(2)log ₂(m) erhält man somit:

Es handelt sich um die Information (im Sinne von Shannon). In der Thermodynamik wählt man:

Daraus folgt:

Entropie:

Öffnet man das Ventil zu einem weiteren Gefäß, steigt die Entropie an, es gilt S > 0, weil Abweichungen von der Gleichverteilung sehr unwahrscheinlich sind. Der Prozeß ist spontan nicht umkehrbar. Die Entropie ist eine extensive Größe: Es gilt die Umrechnung:

Beispiel:

Daraus folgt für die Entropie:

Diese Zahl kann man sich sehr gut merken!

Beispiel (Entropie):

Mit S = -k_BN _np_n lnp_n folgt:

Die absolute Angabe von S ist nicht eindeutig, weil sie abhängig von der Wahl von V ist. Bei der Angabe von Entropiedifferenzen fällt V heraus:

Für die Informationsentropie folgt:

Beispiel:Mischungsentropie

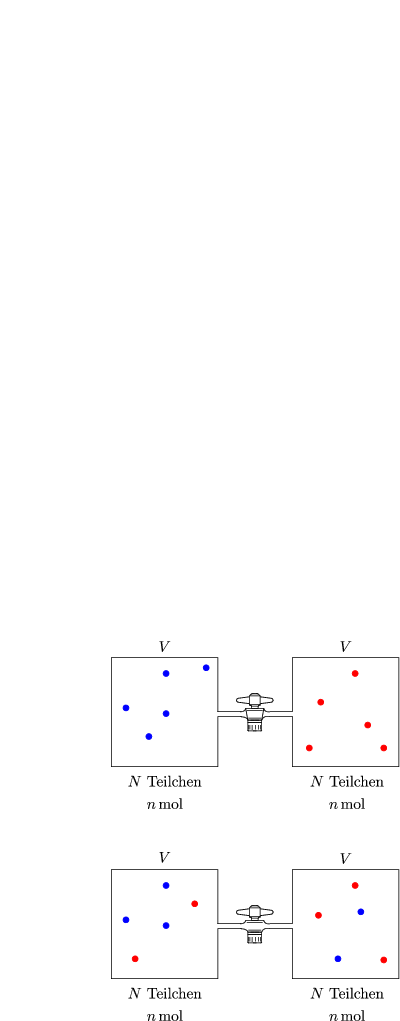
Beziehungsweise gilt:

Die Mischungsentropie taucht natürlich nur dann auf, wenn man verschiedene Gase betrachtet.