6.2 Freies Elektronengas

Wir berechnen die Zustandsdichte der freien Elektronen. Betrachten wir hierzu N Elektronen im Würfel mit dem Volumen L³. Im Kasten gilt für das Potential V = 0 und außen soll das Potential unendlich groß sein. Dazu lautet die Schrödingergleichung:

Als Ansatz zur Lösung nehmen wir ebene Wellen an:

ist hierbei der Wellenvektor. Dann ergeben sich durch Einsetzen folgende Energie-Eigenwerte:

Die erlaubten k-Werte bei endlichem Kristall mit periodischen Randbedingungen (wie bei Phononen) sind:

n ist hierbei eine ganze Zahl.

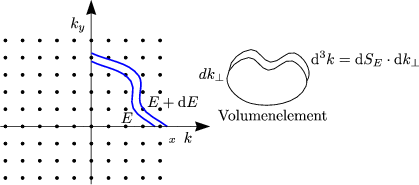
dS_E ist für eine bestimmte Energie ein Flächenelement.

Damit erhalten wir für die Zustandsdichte:

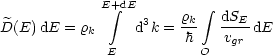
Hier liegt dann wieder eine van-Hove-Singularität vor, falls E(k) flach ist (Vorgriff). Für freie Elektronen ist die Fläche E = const. eine Kugelfläche, da alle k isotrop sind:

Durch Integration über das Flächenelement erhalten wir die Oberfläche einer Kugel:

Wir schreiben das Integral bezüglich der Energie E:

Und damit ergibt sich dann die Zustandsdichte:

Aufgrund des Pauli-Prinzips dürfen nur zwei Elektronen im selben Zustand auftreten. Damit folgt die Zustandsdichte pro Volumen:

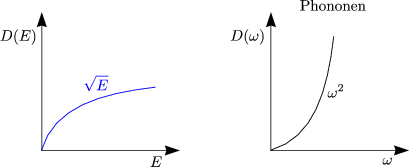
Kommen wir nun zur thermischen Besetzung. Für Teilchen mit ganzzahligem Spin wie beispielsweise Phononen, Photonen und ⁴He gilt die Bose-Einstein-Statistik:

Das chemische Potential ist hierbei definiert als:

Bei manchen Teilchen wie Phononen und Photonen ist das chemische Potential gleich 0, da diese nicht wechselwirken; ihnen ist es praktisch egal, ob noch ein anderes Teilchen hinzukommt. Bei ⁴He jedoch verschwindet das Potential nicht. Für Teilchen mit halbzahligem Spin, sogenannte Fermiteilchen (beispielsweise ³He, Elektronen e), gilt das Pauli-Prinzip. Hier liegt die Fermiverteilung vor:

Für E - » k_BT gehen n(E) und f(E) über in die BOLTZMANN-Verteilung. Die Fermiverteilung für T0 ist:

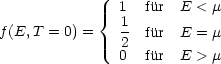
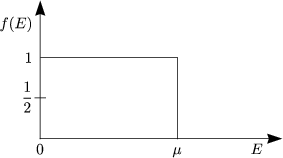
Es sind somit alle Zustände besetzt bis zur „Fermienergie“ E_F = (T = 0). E_F ist durch die Elektronendichte n = festgelegt, da alle Elektronen bis zur Fermienergie besetzt sein müssen.

Daraus folgt dann:

Mit E_F = und den bekannten Impulszusammenhängen mv_F = k_F ergibt sich der sogenannte Fermi-Wellenvektor (Fermi-Wellenzahl) k_F = (3²n) oder die Fermi-Geschwindigkeit v_F = (3²n). Des weiteren läßt sich eine Fermi-Temperatur bestimmen, nämlich T_F = . Die Zustandsdichte bei E = E_F lautet dann: D(E_F) = .

Element	n	kF	vF	EF [eV]	TF [K]
Li	4,7 . 1022	1,1	1,3 . 106	4,7	55000
Na	2,7 . 1022	0,9	1,0 . 106	3,2	38000
Al	1,8 . 1023	1,8	2,0 . 106	11,7	136000
Cu	8,5 . 1022	1,4	1,6 . 106	7,0	82000
Ag	5,9 . 1022	1,2	1,4 . 106	5,5	64000

Ist T_F viel größer als die Schmelztemperatur ( einige 10⁴ K bzw. einige eV), so sind die freien Elektronen im k-Raum gleichmäßig verteilt bis k_F; man bezeichnet diese Verteilung auch als Fermikugel. Die Oberfläche diese Kugel ist die Fermifläche; die Größenordnungen sind: k_F 1Å^-1 und v_F 10⁶ . Für endliche Temperaturen ergibt sich eine Aufweichung in der Fermiverteilung mit einer Breite 2k_BT. Bei f = (also E = ) hängt folgendermaßen von der Temperatur ab:

Die Näherung ist sehr gut für alle üblichen Temperaturen.