6.3 Eigenschaften im Modell „freie Elektronen“

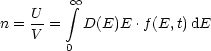
Die spezifische Wärme einfacher Metalle läßt sich über die innere Energie berechnen:

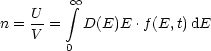
Bei T = 0 findet man dann, wobei wir f(E,T) bis zur Fermienergie E_F durch eins ersetzen können:

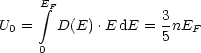
E_F beträgt xeV. Bei Zimmertemperatur 300K ist dies eV. Diese ist riesig verglichen mit Gas bei 300K. Für die spezifische Wärme kommt nur ein kleiner Anteil in Frage:

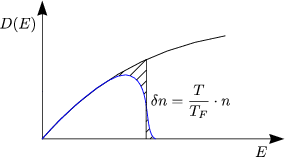
Der Energiezuwachs für jedes dieser Elektronen ist E k_BT, womit sich ergibt:

Damit folgt außerdem:

Man kann diese Berechnung jedoch auch genauer durchführen. Dazu schreiben wir:

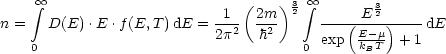
Dieses Integral ist jedoch leider analytisch nicht lösbar. Für k_BT « E_F können wir folgende Näherung machen:

Damit können wir die spezifische Wärme schließlich bestimmen:

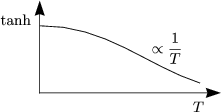
Der erste Faktor folgt durch „Reduktion“ wegen der Fermistatistik. Der zweite Term beschreibt einen freien Gasanteil. Man muß sich deshalb merken C_V ^el T! Dies gilt bei „allen“ Temperaturen. Die Temperaturbereiche, für welche dies nicht mehr gilt, sind experimentell meistens sowieso unzugänglich. Die gesamte spezifische Wärme eines Metalls ergibt sich durch Addition des Anteil durch die Phononen und des Anteils der Elektronen:

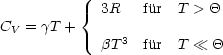
und sind hierbei übliche Abkürzungen. Für hohe Temperaturen dominiert folglich der 3R-Anteil. In der folgenden Schreibweise wird verdeutlicht, daß die Wärmekapazität von der Masse und Dichte der Elektronen abhängt:

Obwohl wir eine sehr einfache Theorie benutzen, stimmen die theoretischen Werte mit den experimentellen gut überein.

	Li	Na	Al	Cu	Ag
exp	1,63	1,38	1,35	0,70	0,65
exp/theo	2,18	1,26	1,48	1,38	1,00

Bekannt sind sowohl n als auch m. Experimentell variiert der Quotient aus _exp und _theo von etwa 1 bis 2. Der Unterschied wird durch Einführung einer effektiven Massen m_th^* („th“ thermisch) berücksichtigt.

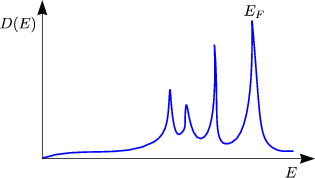
m^* spiegelt also die Wechselwirkung mit dem Gitterpotential wider. Bei den Übergangsmetallen ist m_th^* oft sehr groß. Bei Nickel gilt beispielsweise m_th^* = 15m. Wegen den d-Elektronen sieht hier nämlich die Zustandsdichte anders aus:

6.3.1 Paulische Spinsuszeptibilität

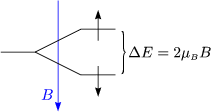
Im thermischen Gleichgewicht gilt:

Die Besetzungszahldifferenz ist dann gegeben durch:

Es gibt für hohe T eine Magnetisierung (_BB « k_BT).

Die Suszeptibilität beträgt daher:

Beispielsweise gilt dann für Natrium mit n(Na) bei 300K, daß 6,9 ^. 10^-4 ist. Experimentell erhält man jedoch einen Wert von = 8,3 ^. 10^-6 T⁰. Unsere Theorie ist damit falsch für freie Elektronen (aber korrekt für paramagnetische Ionen, Curie-Gesetz). Deshalb berücksichtigen wir nun das Pauli-Prinzip:

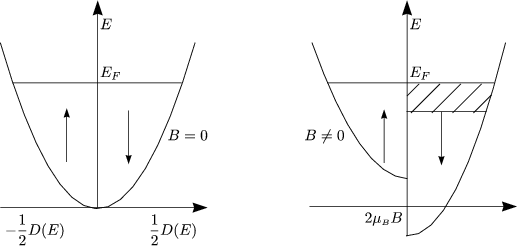
Überschuß von Elektronen mit Spin antiparallel zu B, parallel zu B. Wegen _BB « E_F gilt D(E E_F) const. Daraus erhalten wir für den Überschuß der Elektronen:

Dieses Verhalten entspricht damit dem Experiment. Man spricht auch vom Pauli-Paramagnetismus. Weitere Korrekturen erhält man durch Berücksichtigung des Bahn-Diamagnetismus und der effektiven Masse m^*.

Das Fazit ist also, daß das freie Elektronengas/Fermigas eine gute Sache für einfache Metalle ist.

• Natrium: 1 Elektron/Atom
• Beryllium: 2 Valenzelektronen/Atom

Führt man aber eine Messung der Ladungsträgerkonzentration durch den Halleffekt durch, so stellt man fest, daß der Wert für Natrium stimmt. Im Beryllium verhalten sich die Elektronen jedoch so, als wären sie positiv. Man mißt positive Ladungsträger pro Atom.