Betrachten wir das Potential V (![]() ) = V (
) = V (![]() +
+ ![]() ), wobei
), wobei ![]() irgendein Gittervektor ist.
Wir notieren uns die stationäre Schrödingergleichung für dieses Problem:
irgendein Gittervektor ist.
Wir notieren uns die stationäre Schrödingergleichung für dieses Problem:
![]() ist hierbei ein reziproker Gittervektor. Man macht für die Wellenfunktion einen
Ansatz durch Entwicklung nach ebenen Wellen:
ist hierbei ein reziproker Gittervektor. Man macht für die Wellenfunktion einen
Ansatz durch Entwicklung nach ebenen Wellen:
Man summiert über alle möglichen ![]() -Vektoren, also über diese, welche mit den
periodischen Randbedingung kompatibel sind.
-Vektoren, also über diese, welche mit den
periodischen Randbedingung kompatibel sind.
Durch Einsetzen in die Schrödingergleichung:
Wir benennen ![]() '
+
'
+ ![]() in
in ![]() um:
um:
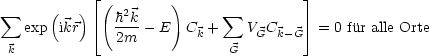
Für jedes erlaubte ![]() muß der Ausdruck in der Klammer gleich 0 sein.
muß der Ausdruck in der Klammer gleich 0 sein.
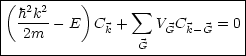
Es handelt sich um die Schrödingergleichung im k-Raum für die Koeffizienten C![]() .
Durch die Vereinfachung wegen der Periodizität von V (
.
Durch die Vereinfachung wegen der Periodizität von V (![]() ) ergibt sich
) ergibt sich ![]()
![]()
![]()
![]()
![]() für jedes
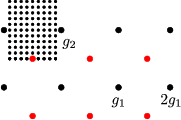
für jedes ![]() innerhalb der 1.Brillouin-Zone. Es liegt damit eine Kopplung Ck mit allen
möglichen Ck-
innerhalb der 1.Brillouin-Zone. Es liegt damit eine Kopplung Ck mit allen
möglichen Ck-![]() vor (rote Punkte). Die Wellenfunktion ist also von folgender
Struktur:
vor (rote Punkte). Die Wellenfunktion ist also von folgender
Struktur:
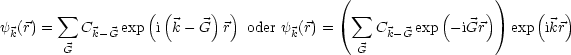
exp![]() stellt eine ebene Welle dar und uk(
stellt eine ebene Welle dar und uk(![]() ) ist eine gitterperiodische
Modulation.
) ist eine gitterperiodische
Modulation.
uk(![]() ) ist
) ist ![]() -spezifisch (
-spezifisch (![]() modulo
modulo ![]() ).
). ![]() ist ein beliebiger Gittervektor. Dies ist ein
sehr wichtiges Theorem, nämlich das sogenannte Bloch-Theorem:
ist ein beliebiger Gittervektor. Dies ist ein
sehr wichtiges Theorem, nämlich das sogenannte Bloch-Theorem:
| Wellen im periodischen Potential haben diese Form; man bezeichnet sie als Bloch-Wellen. |
Wir wollen uns nun noch etwas mit diesen Bloch-Wellen beschäftigen. Diese besitzen zwei Symmetrieeigenschaften:
Eine Translation um ![]() entspricht einer Multiplikation mit einem
Phasenfaktor exp(i
entspricht einer Multiplikation mit einem
Phasenfaktor exp(i![]()
![]() . Dies kann folgendermaßen gezeigt werden, wobei
wir auf Vektorpfeile verzichten wollen:
. Dies kann folgendermaßen gezeigt werden, wobei
wir auf Vektorpfeile verzichten wollen:
Dies ist eine oft alternative Formulierung des Bloch-Theorems. In diesem Zusammenhang wollen wir nochmal zurückblicken auf elastische Wellen: Diese sind im Grunde genommen auch einfache Bloch-Wellen mit dem Vorfaktor uq(r) = Uq = const. Sonst gibt es keine explizite r-Abhängigkeit „zwischen“ den Atomen.
Hier liegt eine Periodizität mit ![]() vor. Besitzt eine Blochwelle die
Wellenzahl k' = k + G', so stellt man fest, daß diese identisch mit einer
Blochwelle der Wellenzahl k ist. Auch dies können wir zeigen:
vor. Besitzt eine Blochwelle die
Wellenzahl k' = k + G', so stellt man fest, daß diese identisch mit einer
Blochwelle der Wellenzahl k ist. Auch dies können wir zeigen:
Wir bezeichnen nun G'-G mit G''. Da man sowieso über alle G summiert, kann mann auch über alle G'' summieren:
An einer Blochwelle mit bestimmten k sind (schon) alle möglichen k + G beteiligt. Aber außerhalb der 1.Brillouin-Zone gibt es nichts neues. Diese Periodizität kann sich nicht nur auf die Wellenfunktion beziehen, sondern muß sich auch in den Eigenwerten äußern. Man stellt fest, daß Ek periodisch mit G ist. Die Ek stellen Energieflächen im k-Raum dar. Die Gesamtheit dieser k’s bezeichnet man als „elektronische Bandstruktur“.
Da nun ![]() k gitterperiodisch ist, gilt
k gitterperiodisch ist, gilt ![]() k+G =
k+G = ![]() k und damit erhalten wir
die Eigenwertgleichung:
k und damit erhalten wir
die Eigenwertgleichung:
Es gilt also Ek = Ek+G und damit ist auch E gitterperiodisch. Es ist damit eine Beschränkung auf die erste Brillouin-Zone möglich (reduziertes Zonenschema).