6.5 Näherung für quasifreie Elektronen

Die Idee ist, daß man nur ein äußerst schwach moduliertes Potential hat. Man erwartet nur dann merkliche Effekte, wenn die Wellenlänge (oder Vielfache) der elektronischen Wellenfunktion mit der Gitterperiodizität übereinstimmen. Wir betrachten zunächst V () = V ( + )0. Diesen Fall bezeichnet man auch als „leeres Gitter“ mit Translationsinvarianz. Es liegen also freie Elektronen vor, aber es müssen nach wie vor Blochwellen auftreten:

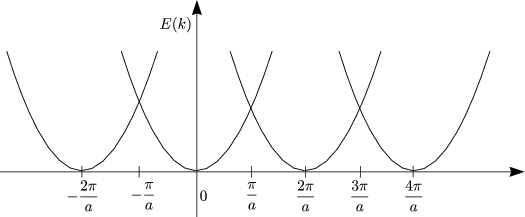
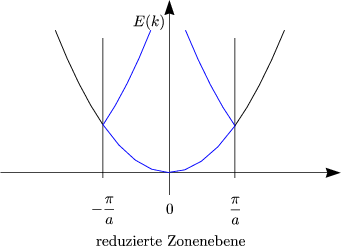
Bei einem schwachen Potential findet eine Aufhebung der Entartung statt bei k = + G (eindimensionaler Fall). Daraus ergibt sich, daß die Hauptbeiträge von Lösungen, die zu C und C_- gehören und die Beiträge zu anderen vernachlässigbar sind. Dadurch, daß wir nur noch Beiträge haben mit C und C_- bezeichnet man diese auch als „Zwei-Komponenten-Lösung“.

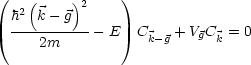
V _g ist hierbei die erste Fourierkomponente von V (). Führen wir dann noch die Energiewerte des leeren Gitters an:

Durch Lösen dieses Gleichungssystems erhalten wir:

An der Zonengrenze gilt k = und E_{k - g}⁰ = E_k⁰. Damit folgt:

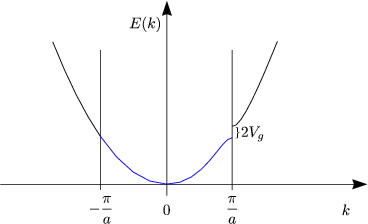
Anschaulich gilt:

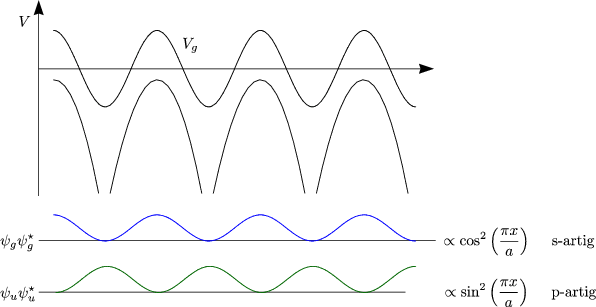
In der Nähe der Zonengrenze können wir E_k um k = entwickeln:

||² ist parabolisch und besitzt eine horizontale Tangente.