6.6 Näherung für quasigebundene Elektronen („tight binding“)

Es liegen atomare Wellenfunktionen mit einem schwachen Überlapp vor. Die Diskussion dieses Problems funktioniert ähnlich wie bei der kovalenten Bindung. Damals hatten wir das LCAO-Modell (linear combination of atomic orbitals) betrachtet. Wir nehmen also an, daß das atomare Problem gelöst sei:

In einem Kristall wollen wir die Einelektronen-Näherung durchführen. Wir betrachten ein Elektron m im Gesamtpotential V = V _a + v.

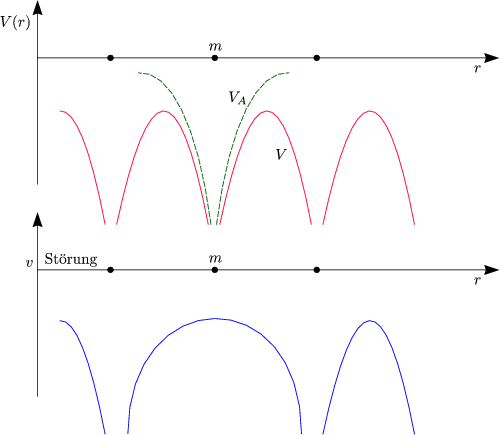
Hierbei handelt es sich um eine Summe über alle anderen Atome. Zu lösen ist dann das Eigenwertproblem:

(r) müssen bekanntlich wieder Bloch-Wellen sein. Die Energie-Eigenwerte, wenn wir die Wellenfunktion _k kennen, können berechnet werden durch:

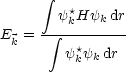
Die Idee ist nun wieder das Ritzsche Variationsverfahren mit einer Versuchsfunktion _k. Dann muß gelten:

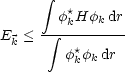
E_k kann als Minimum angenähert werden durch Variation von eben dieser Versuchsfunktion . Versuch: sei eine lineare Überlagerung der Atomwellenfunktionen ( -), wobei wir die Vektorpfeile wieder weglassen wollen:

An dieser Stelle nützen wir nun aus, daß es sich um eine Blochwelle handelt, da ja ein periodisches Gitter vorliegt. Diese Bloch-Welle muß aus einer gitterperiodischen Modulation und einen Phasenfaktor (Wellenanteil) bestehen. Der gitterperiodische Anteil muß hierbei in der Summe über die stecken und der Phasenfaktor in den a_m. Wir schreiben also die Versuchsfunktion auf als:

Damit können näherungsweise die Energiewerte E_k berechnet werden.

Wir betrachten als lineare Überlagerung der Atomwellenfunktionen ( -).

Dies muß eine Blochwelle (=gitterperiodische Modulation × Phasenfaktor), also verwenden wir die Versuchsfunktion:

Jetzt berechnen wir E_k näherungsweise. Dazu berechnen wir den Nenner des Bruches:

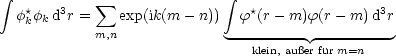
Bei starker Lokalisierung sind nur Glieder mit m = n wichtig und daher kann folgende Näherung benutzen:

Damit erhalten wir:

i ist der Index der atomaren Wellenfunktion. Wendet man H_A auf die linke komplex konjugierte Wellenfunktion ^*(r - m) an, so erhält man die atomaren Eigenwerte E_i für m = n. Wir spalten das ganze in zwei Anteile A_i und B_i auf:

Hierbei handelt es sich um die Energieabsenkung mit Bezugselektron m aufgrund von v.

Dies ist ein Überlappintegral vom Bezugselektron m mit Nachbarn n. Durch Summation über m ergibt sich jeweils ein Faktor N:

P_ni beschreibt die Geometrie der Umgebung (Gitterstruktur). Die Summe über die nächsten Nachbarn ist hierbei meist ausreichend. Als Beispiel betrachten wir den einfachsten Fall, nämlich daß kugelsymmetrisch ist. Wir betrachten nur die nächsten Nachbarn eines kubisch primitiven Gitters. Dieses besitzt genau 6 nächste Nachbarn:

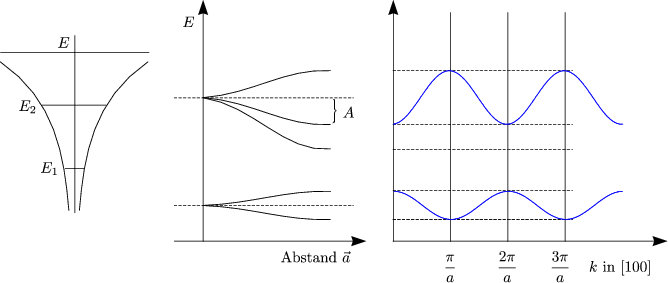
A_i beschreibt die globale Energieabsenkung. Der Bandindex B_i bestimmt die Breite des Bandes. A_i und B_i hängen im allgemeinen von i ab. Betrachten wir E_k bei k = 0:

Bei k = gilt:

Vergleiche dies mit E = beim freien Elektron. Die effektive Masse m_i^* = ± kann sehr verschieden von m₀ sein. Als Beispiel kann man hier den Ionenkristall K⁺Cl^- anführen. Hier ist der Überlapp klein, weshalb somit die Bänder schmal sind. Bei kleinem Überlapp ist auch der Faktor B_i klein und damit wird auch die Breite der Oszillationen klein.

Bei kovalenten Bindungen, wie diese beispielsweise im Diamant auftreten, entstehen aus s- und p-Orbitalen sogenannte sp³-Hybride (im Festkörper). Bei 4 Elektronen pro Atom im Valenzband erhält man E_Lücke 1eV für Si und etwa 5eV für C.