Dies ist das Fundament für die Dynamik des Wellenpakets der Kristallelektronen. Die Gruppengeschwindigkeit ergibt sich aus:
Die äußere Kraft ergibt sich aus 
= 
(Quasiimpulsänderung). Die En(
)-Flächen
bestimmen alles! Betrachten wir nun:
Der Wellenvektor ist gegeben durch:
![˙ -e [ ]
k = ---E(r,t)+ vn(k)× B(r,t)
h](ex855x.gif){kind=small}
unbestimmt modulo G:
Elektron (n, 
, 
) 
Elektron (n, 
+ 
, 
)
Die Felder sind schwach; beispielsweise gilt 
» a, 
« Bandlücke
(Dynamik, Beschleunigung). Damit gilt für die x-Komponente:
Vergleiche dies mit der klassischen Bewegungsgleichung 
= 
F.
Betrachten wir die Komponente i:
Der effektive-Masse-Tensor wird definiert mit der dynamischen Masse:
Krümmung der Ek-Flächen ist entscheidend. Die Beschleunigung
im Gitterpotential ist parallel zur Kraft. Die 
ij-Tensoren sind
symmetrisch, es ist damit eine Hauptachsentransformation möglich.
In parabolischen Bandabschnitten (Oberkante, Unterkante) wird mij*
unabhängig von |
|. Sie kann aber noch von der Richtung abhängen.
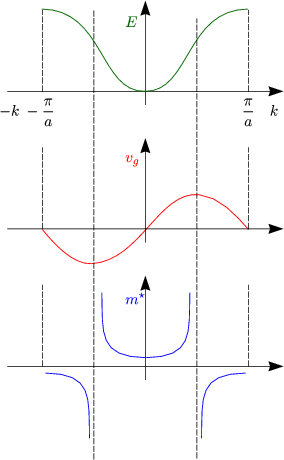
Die Bandkrümmung bei -
ist größer als bei k ~ 0. Damit muß gelten:
Betrachten wir die Bewegung im Ortsraum mit 
= -e
, wobei das
elektrische Feld 
konstant sein soll. Außerdem gelte 
> 0 = const., wobei das
Teilchen bei x 
0 starten soll:
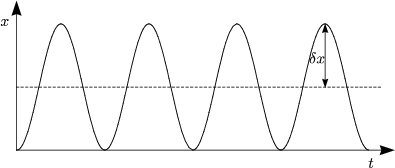
Die Kristallelektronen oszillieren bei konstantem elektrischen Feld! Man bezeichnet diese Schwingungen als „Bloch-Oszillationen“. Wir machen folgende Abschätzung: Bei der einmaligen Bewegung durch die Brillouinzone gilt:
Hierbei ergeben sich folgende Resultate:
t bei E 
100
beträgt etwa 200ms. Die
mittlere Geschwindigkeit v liegt in der Größenordnung von der
Fermigeschwindigkeit 106 
.
x v
10cm!
Bei realen Materialien betragen die Stoßzeiten 10-12 - 10-14 s! Damit ergibt
sich x 1
m bis 10nm. Stöße sind entscheidend für das Verständnis von
Transportphänomenen. Blochoszillationen werden in speziell präparierten
HL-Heterostrukturen beobachtet. Ladungstransport in Banden, Elektronen und
Löcher
Der Strombeitrag der Kristall-Elektronen zwischen 
und 
+ d
beträgt:
Der Vorfaktor ergibt sich durch die Dichte 
im 
-Raum, wobei
zwei Spinrichtungen berücksichtigt werden müssen. Damit gilt für die
Stromdichte:
Mit E(
) = E(-
) ergibt sich 
(
) = -
(-
) und damit j = 0 ohne Feld.
Mit Feld ist für alle 
+ 
der Zustand stationär wegen Stößen.
Bei vollen Bändern bleibt die Kompensation perfekt. Es ergibt sich
j = 0, womit ein Isolator vorliegt. Bei teilgefüllten Bändern ist die
Kompensation unvollständig; dann gilt j
0 und es findet Ladungstransport
statt.
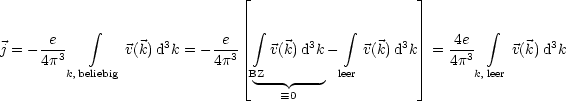
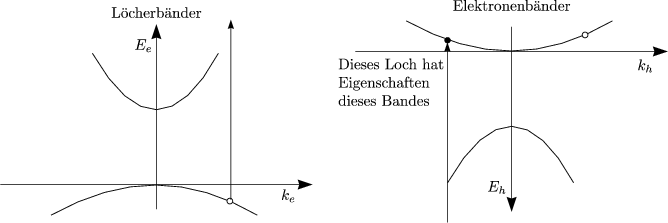
Es handelt sich um besetzte Zustände mit positiver Ladung. Diese
Quasiteilchen bezeichnet man als Defektelektronen oder auch Löcher. Dieses
Konzept ist hilfreich bei fast vollen Banden in Halbleitern. Betrachten wir nun
die Eigenschaften von Löchern („holes“): Ein Loch ergibt sich durch ein volles
Band minus 1 Elektron bei 
e.
Im Elektronenband gilt dann:
h = -
e.
Dies entspricht einem besetzten Loch im Lochband. Je tiefer Ee(
)
des entfernten Elektrons ist, desto höher ist die Energie des Systems.
) = -Ee(
)
Aus 
kEh(k) = 
kEe(k) ergibt sich 
h = 
e.
