Kapitel 7
Bewegung von Ladungsträgern, Transportphänomene
Blochwellen sind
zur Beschreibung ungeeignet, weil es sich um Eigenzustände handelt. Wir führen
deshalb Wellenpakete ein. Dazu betrachten wir die Mittelwerte 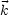 ,
, 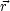 mit den
Unschärfen
mit den
Unschärfen  k,
k,  r
r  1. Ein freies Elektron kann durch eine Summe aus ebenen
Wellen beschrieben werden:
1. Ein freies Elektron kann durch eine Summe aus ebenen
Wellen beschrieben werden:
![[ ( )]
sum ' ' h2k2 h2k2
y(r,t) = 'g(r) exp i k r- 2m t mit E = 2m = hw
k](ex844x.gif)
Es gilt g(k')  0 für |k'- k| >
0 für |k'- k| >  k. Ein Kristall-Elektron (Bloch-Elektron) kann als
Summe von Blochwellen geschrieben werden:
k. Ein Kristall-Elektron (Bloch-Elektron) kann als
Summe von Blochwellen geschrieben werden:
![[ ( )]
sum ' En(k')-
yn(r,t) = ' g(k )yn,kexp -i h t
k](ex845x.gif)
n bezeichnet man als Bandindex und 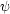 n,
n,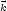 ist eine Blochwelle.
ist eine Blochwelle. 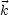 muß „gut“
definiert sein (
muß „gut“
definiert sein ( k «
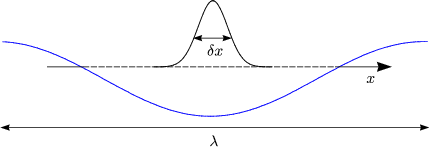
k «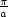 ). Daraus ergibt sich a «
). Daraus ergibt sich a «  x «
x «  (Wellenlänge externer
Felder).
(Wellenlänge externer
Felder).
![]() 0 für |k'- k| >
0 für |k'- k| > ![]() k. Ein Kristall-Elektron (Bloch-Elektron) kann als
Summe von Blochwellen geschrieben werden:
k. Ein Kristall-Elektron (Bloch-Elektron) kann als
Summe von Blochwellen geschrieben werden:
![]() n,
n,![]() ist eine Blochwelle.
ist eine Blochwelle. ![]() muß „gut“
definiert sein (
muß „gut“
definiert sein (![]() k «
k «![]() ). Daraus ergibt sich a «
). Daraus ergibt sich a « ![]() x «
x « ![]() (Wellenlänge externer
Felder).
(Wellenlänge externer
Felder).
