Wir betrachten die Eindeutigkeit der Wellenfunktion beim Umlauf. Das 
-Feld sei
gegeben durch 
= (0,0,B) und die Bewegung in x-Richtung sei an die Bewegung in
y-Richtung gekoppelt. Wir wissen aus der theoretischen Physik, daß kx und ky keine
guten Quantenzahlen sind. Die Schrödingergleichung für ein freies Elektron im
Magnetfeld lautet dann:
Wir machen einen Ansatz nach LANDAU: 
= 
(x)exp[i(kyy + kzz)] und führen
folgende Koordinatentransformation durch:
Daraus ergibt sich dann eine Gleichung für :
![|-2-------[------------]------|
|@-f-+ 2m- E'- 1mw2 x'2 f = 0|
-@x'2---h-------2---e---------|](ex1066x.gif){kind=small}
Hierbei handelt es sich um die Differentialgleichung eines linearen Oszillators mit der
Eigenfrequenz 
C. Das Zentrum liegt bei x0 = 
und die Eigenwerte sind gegeben
durch:
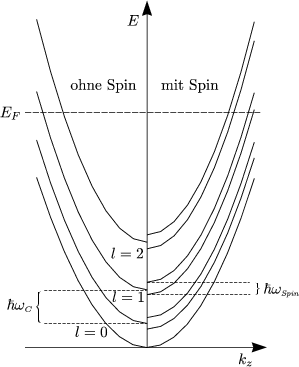
Die Subbänder heißen LANDAUniveaus.
Die Bahnen sind anschaulich Kreisbahnen im Ortsraum:
Die Energie beträgt
und damit ergibt sich die eingeschlossene Fläche
Im k-Raum liegen auch Kreisbahnen vor:
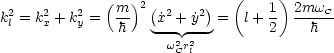
Für die Fläche gilt:
Die Quantisierung wird geändert von kx, ky 
kl2.
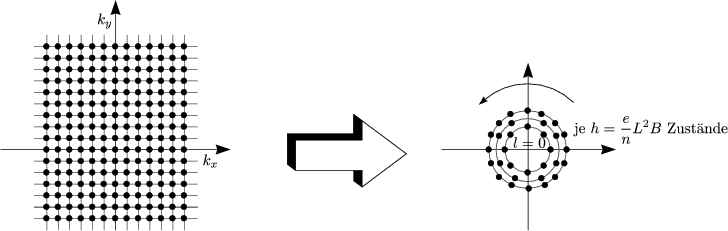
Betrachten wir eine dreidimensionale Veranschaulichung mit kz:
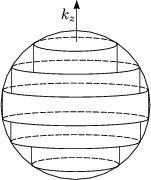
Die LANDAU-Röhren sind besetzt bis EF. An dieser Stelle wollen wir den DE HAAS-VAN ALPHEN-Effekt:
 |  |
|
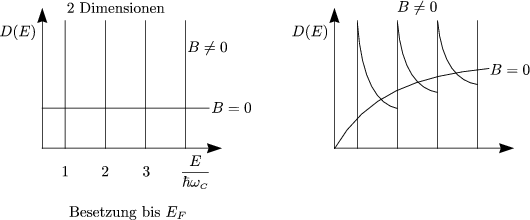
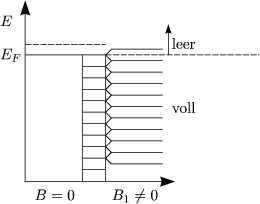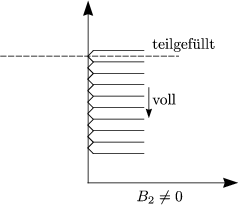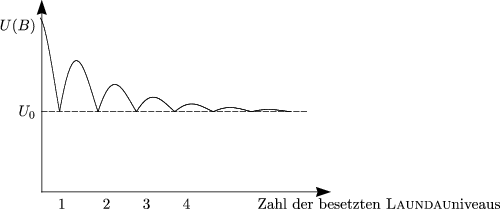
| So, daß alle LANDAUniveaus voll oder leer | Etwas größer als B1 | |
| Innere Energie U0 | U1 = U0 (selten) | U2 > U0 („Normalfall“) |
Der seltene Fall U1 = U0 passiert immer, wenn EF(B = 0) = 
C 
p . .
Mit U verknüpft ist die spezifische Wärme und die elektrische Leitfähigkeit. (SHUBNIKOV-DE-HAAS-Oszillationen) Die Magnetisierung ist gegeben durch:
DE-HAAS-VAN-ALPHEN-Effekt
