7.3 Thermische Leitfhigkeit von Metallen

7.3 Thermische Leitfähigkeit von Metallen

Wir führen als erstes ein Vergleich mit Isolatoren (das heißt nur Phononentransport) durch. Die Erfahrung zeigt, daß bei hohen Temperaturen $/\$ _el » $/\$ _ph gilt. Ein Metall leitet die Wärme also besser als ein Isolator. Bei tiefen Temperaturen gilt $/\$ _el » $/\$ _ph wegen C_V,el T, C_V,el T³. Mit der kinetischen Gastheorie findet man $/\$ _el = C_V^elvl. Betrachtet man nur die Fermifläche, so gilt:

1 p2nk2BT- /\el = 3 mv2 vFl F

Wir vergleichen dies mit der elektrische Leitfähigkeit:

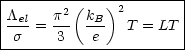
|----------------------| /\el p2 (kB )2 | --- = --- --- T = LT | -s-----3---e------------

Man bezeichnet dieses als WIEDEMANN-FRANZ-Gesetz. L ist die LORENZ-Zahl, für die L = 2,5 ^. 10^-8 gilt. Handelt es sich hier um eine universelle Konstante? Dies ist bemerkenswert, aber nur sinnvoll, wenn gleiche Streuprozesse bei für und bei für $/\$ wichtig sind. Man stellt fest, daß für Cu gilt:

-/\- { const. ~~ L f¨ur T > 100K sT = const.< L f¨ur T < 10K

Dazu betrachten wir die elektrische Leitfähigkeit:

( ) f(k) = f0(k+ dk) = f0 E(k)+ etv(k)E mit dk = etE und dE = dEdk h dk

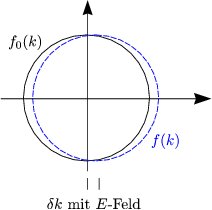
Dies ist die linearisierte BOLTZMANNgleichung.

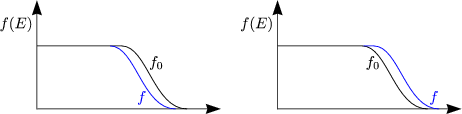
f behält die Form. Besonders effektiv bei der Streuung sind die sogenannte „horizontalen“ Streuprozesse, bei denen der Impulsübertrag gerade wichtig ist.

Elektronen von warm kalt	Elektronen von kalt warm

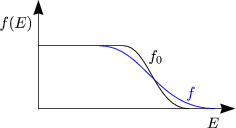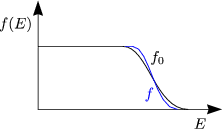Hier sind sogenannte „vertikale“ Streuprozesse wichtig mit Energiebeitrag (inelastisch), wobei der Impulsbeitrag unwichtig ist. Wir betrachten die BOLTZMANNgleichung für den thermischen Transport mit Diffusionsterm statt Feldterm:

( ) f(T) = f0 T - tv(k) \~/ T = f0(T - dT)

Die Elektronen sind „wärme“ oder „kälter“ je nach Flugrichtung bezogen auf den Gradienten der Temperatur $\~/$ T.

7.3.1 Thermoelektrische Effekte

Für die BOLTZMANN-Gleichung gilt:

f(k) = f0(k)+ e-tE \~/ kf - tv \~/ f h

Mit dem Relaxationsansatz kann man diese linearisieren:

f(k) ~~ f (k)+ et E \~/ f - t@f0v \~/ T 0 h k 0 @T

Man erhält also:

e integral @f0 @T jx = sEx - 4p3 t(k)v2x@T- .@x-

Dies hatten wir abgeleitet mit E_F = const. (ortsunabhängig). Dies ist in Ordnung bei Metallen; im allgemeinen kann jedoch E_F = E_F() bei 0 gelten. Dies ist insbesondere bei Halbleitern der Fall, wenn die Elektronendichte und die Fermienergie klein sind. Allgemein kann man schreiben:

( ) j = sE' + L2 -@T- mit E' = E + 1 \~/ E (r) x x xx @x x x e F

Es gibt damit immer eine Kopplung des Wärmestroms mit dem elektrischen Transport.

J = L11E'+ L12(- \~/ T )

21 ' 22 JQ = L E + L (- \~/ T )

L^ij sind die Transportkoeffizienten; es handelt sich im allgemeinen um Tensoren.

7.3.2 SEEBECK-Effekt

Mit j = 0 erhalten wir:

12 Ex = L-11 @T-= S@T- L @x @x

S nennt man absolute Thermokraft innerhalb eines Metalls.

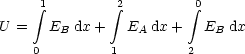
integral 1 integral 2 integral 0 U = EB dx + EA dx+ EB dx 0 1 2

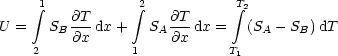
integral 1 @T integral 2 @T integral T2 U = SB @x-dx+ SA@x-dx = (SA- SB) dT 2 1 T1

7.3.3 PELTIER-Effekt

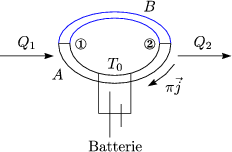
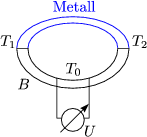
Man legt hierbei ein „Sinus-Material“ durch. (Bei einem Leiter spricht man von einem freien Sinus-Material; durch Verzweigung entsteht ein Kosinus-Material.) Es gelte = 0 und wir erhalten mit j = L¹¹E, j_Q = L²¹E:

21 jQ = L- j = p .j L11

ist der PELTIERkoeffizient.

An Punkt 1 Wärmesenke: (_A - _B)j = Q₁ (wird kälter)
An Punkt 2 Wärmequelle: (_A - _B)j = Q₂ (wird wärmer)

[next] [prev] [prev-tail] [front] [up]