Historisch: DRUDE hat sich hier um 1900 Gedanken gemacht. Elektronen kann man
als klassisches Gas behandeln, für welche die MAXWELL-BOLTZMANN-Statistik gilt
mit vth, wobei vth = 0 ist. Es finden hierbei viele Stöße statt, wobei die mittlere
Stoßzeit ![]() ist. Für ein elektrische Feld
ist. Für ein elektrische Feld ![]() ergibt sich:
ergibt sich:
Nach jedem Stoß gelte v = 0. Damit ergibt sich:
![]() ist hierbei die sogenannte Beweglichkeit.
ist hierbei die sogenannte Beweglichkeit.
Diese Konzept ergibt eine vernünftige Übereinstimmung mit dem Experiment; dies ist aber falsch!
Damit folgt eine äußere Kraft mit ![]()
![]() =
= ![]() (beispielsweise für
(beispielsweise für ![]() = e
= e![]() ).
).
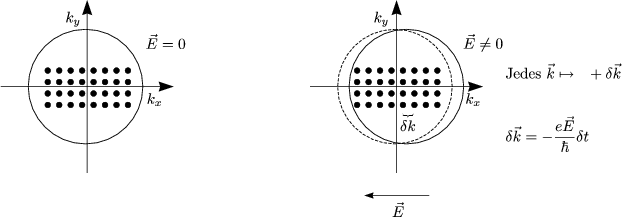
Es liegt damit ein Ungleichgewicht vor, womit eine Streuung in freie Zustände nach
„hinten“ stattfindet. Es ergibt sich ein „Stillstand“ nach ![]() . Für stationäre k gibt es
eine kleine „Schicht“ 2
. Für stationäre k gibt es
eine kleine „Schicht“ 2![]() k (vorne
k (vorne ![]() , hinten
, hinten ![]() ), welche nicht kompensiert wird. Ein
Strom entsteht durch wenige, aber schnelle (vF) Elektronen. Was ist nun aber
), welche nicht kompensiert wird. Ein
Strom entsteht durch wenige, aber schnelle (vF) Elektronen. Was ist nun aber
![]() ?
?
Bei kleinen Änderungen können wir eine Linearisierung der Funktion (TAYLOR-Reihe) durchführen:
Mit Stößen muß man einen Korrekturterm einführen.
Diese ist die BOLTZMANN-Transportgleichung. Der erste Term ist der Streuterm, der
zweite der Diffusionsterm, der dritte der Stoß-Streuterm. Der Stoßterm bei der
Streuung von k![]() k' (und rückwärts) ist eigentlich kompliziert. Infolgedessen macht
man pauschal einen sogenannten Relaxationsansatz
k' (und rückwärts) ist eigentlich kompliziert. Infolgedessen macht
man pauschal einen sogenannten Relaxationsansatz
wobei ![]() die sogenannte Relaxationszeit und
die sogenannte Relaxationszeit und ![]() -1 die Streurate ist. Die Änderung ist
praktisch proportional zur Abweichung von einem Gleichgewichtszustand f0(
-1 die Streurate ist. Die Änderung ist
praktisch proportional zur Abweichung von einem Gleichgewichtszustand f0(![]() ).
Damit ist die zeitliche Variation proportional zu exp
).
Damit ist die zeitliche Variation proportional zu exp![]() nach einer stufenförmigen
Änderung. Diskutieren wir an dieser Stelle den Ladungstransport, insbesondere die
elektrische Gleichstromleitfähigkeit:
nach einer stufenförmigen
Änderung. Diskutieren wir an dieser Stelle den Ladungstransport, insbesondere die
elektrische Gleichstromleitfähigkeit:
Die explizite Zeitabhängigkeit von f fällt hier heraus, also gilt ![]() = 0.
= 0.
Damit folgt mit ![]() = -
= -![]() eE:
eE:
Hiermit ergibt sich eine kleine Abweichung von f0(k):
Hieraus ergibt sich die linearisierte BOLTZMANNgleichung:
![]() kf0(k) entspricht den Grad der Gleichgewichtsverteilung statt dem Grad der
tatsächlichen Verteilung. Scheuen wir uns die Stromdichte an:
kf0(k) entspricht den Grad der Gleichgewichtsverteilung statt dem Grad der
tatsächlichen Verteilung. Scheuen wir uns die Stromdichte an:
Der Beitrag der Integration über f0 ergibt Null. Weiterhin betrachten wir den
einfachsten Fall ![]() = (Ex,0,0). Darüber hinaus nehmen wir an, daß ein isotropes
Material vorliegt, daß also jy = jz = 0 gilt.
= (Ex,0,0). Darüber hinaus nehmen wir an, daß ein isotropes
Material vorliegt, daß also jy = jz = 0 gilt.
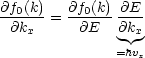
Damit ergibt sich nun:
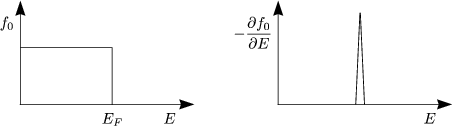
Es gilt also ![]()
![]() -
-![]() (E - EF) und d3k = dk
(E - EF) und d3k = dk
![]() dSF =
dSF = ![]()
![]() dSF:
dSF:
dSF ist hierbei ein Flächenelement auf der Fermifläche. Hier ist zunächst zu Ende
wegen ![]() (
(![]() F). Der einfachste Fall ist:
F). Der einfachste Fall ist:
Hieraus folgt dann für diesen Fall:
Dies bezieht sich ausschließlich auf Elektronen an der Fermikante. Mit
D(EF) = ![]()
![]() , kF = (3
, kF = (3![]() 2n)
2n)![]() und EF =
und EF = ![]() m*vF2 können wir diesen
Ausdruck weiter umformen:
m*vF2 können wir diesen
Ausdruck weiter umformen:
Dieses Ergebnis erhielt auch DRUDE mit einer viel einfacheren
Betrachtung. Beispielsweise erhält man für Kupfer Cu bei 300K mit
![]()
![]() 2.10-14 s, vF
2.10-14 s, vF ![]() 1,6.106
1,6.106 ![]() eine Weglänge von l = vF .
eine Weglänge von l = vF .![]()
![]() 30nm. Bei
4K folgt aus
30nm. Bei
4K folgt aus ![]()
![]() 2.109 s ein Wert von l
2.109 s ein Wert von l ![]() 0,3cm. Dies ist ein Widerspruch
zur Berechnung von DRUDE, welcher l
0,3cm. Dies ist ein Widerspruch
zur Berechnung von DRUDE, welcher l ![]() 10Å erhielt.
10Å erhielt.
Die Ursache von ![]() und
und ![]() (T) sind Streuprozesse durch Defekte, Phononen und
Elektronen.
(T) sind Streuprozesse durch Defekte, Phononen und
Elektronen.
Da viele Elektronen vorhanden sind, könnte man vermuten, daß diese Art der Streuung sehr wirkungsvoll ist. Dies stellt sich jedoch als Irrtum heraus aufgrund des Pauliprinzips. Betrachten wir beispielsweise zwei Kristallelektronen:
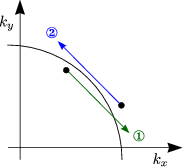
Es sei Elektron 1 oberhalb von EF, also gelte E1 > EF und E2 < EF.
Nach Pauli muß dann E1' > EF und E2' > EF gelten und damit
E1+E2 > 2EF. Mit E1-EF ![]() kBT « EF folgt E2
kBT « EF folgt E2 ![]() EF. Elektron
2 kommt aus der dünnen Schale
EF. Elektron
2 kommt aus der dünnen Schale ![]() des gesamten Raums.
des gesamten Raums.
Für den Impuls gilt ![]() 1-
1-![]() 1' =
1' = ![]() 2'-
2'-![]() 2, wobei Elektron 2 in die dünne
Schale
2, wobei Elektron 2 in die dünne
Schale ![]() übergeht.
übergeht.
Es ergibt sich der Streuquerschnitt
wobei ![]() Str,0 der Streuquerschnitt für ein festes Ion ist. Bei 1K gilt
Str,0 der Streuquerschnitt für ein festes Ion ist. Bei 1K gilt
![]() e-e = 10-10
e-e = 10-10![]() Str,0; pro 1022 Elektronen sind also 1013 geladene Defekte
vorhanden. Diese Anzahl ist im allgemeinen sehr klein und daher wird
dieser Streuprozeß sehr unwichtig (in Schwerfermion-Systemen gibt es
T2-Abhängigkeit).
Str,0; pro 1022 Elektronen sind also 1013 geladene Defekte
vorhanden. Diese Anzahl ist im allgemeinen sehr klein und daher wird
dieser Streuprozeß sehr unwichtig (in Schwerfermion-Systemen gibt es
T2-Abhängigkeit).
Diese ist im allgemeinen statisch; das heißt, es handelt sich um eine elastische
Streuung. Da die Energien gleich bleiben, gilt |![]() '
|
'
|![]() |
|![]() | und für den Impuls
| und für den Impuls
![]() '
=
'
= ![]() +
+ ![]() , wobei
, wobei ![]() beliebig ist und sich aus den Gittereigenschaften
ergibt.
beliebig ist und sich aus den Gittereigenschaften
ergibt.
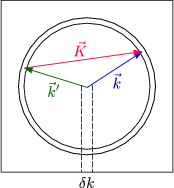
Für die Energie der Phononen gilt Eq ![]() kBT « EF und damit folgt |
kBT « EF und damit folgt |![]() '
|
'
|![]() |
|![]() |.
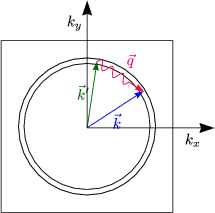
Es sind somit nur Zustände in der Nähe der Fermifläche beteiligt mit
|.
Es sind somit nur Zustände in der Nähe der Fermifläche beteiligt mit
![]() '
=
'
= ![]() ±
±![]() +
+ ![]() , wobei
, wobei ![]() die Phonon-Erzeugung bzw. -Vernichtung beschreibt.
Der Normalprozeß ist der mit G = 0.
die Phonon-Erzeugung bzw. -Vernichtung beschreibt.
Der Normalprozeß ist der mit G = 0.
Für G![]() 0 liegt ein sogenannter Umklappprozeß vor:
0 liegt ein sogenannter Umklappprozeß vor:
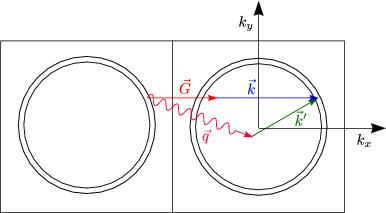
Dieser Prozeß ist wichtig aufgrund des großen Impulsübertrags. Bei kleinem q ist ein minimales q erforderlich. Dies ist abhängig von der allgemeinen Form der Fermifläche und Brillouinzone.
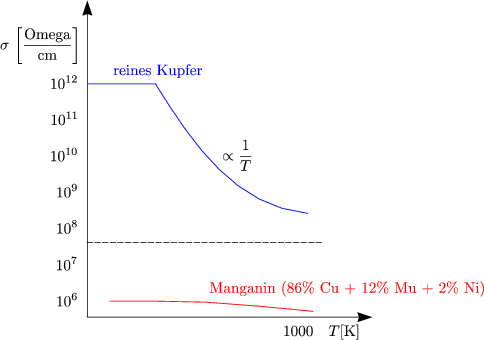
![]() (kF) ist temperaturabhängig und unabhängig von Streumechanismen:
(kF) ist temperaturabhängig und unabhängig von Streumechanismen:
Der effektive Widerstand ist gegeben durch:
Man bezeichnet dieses Verhalten auch als Mathieusche Regel. ![]() D ist ein Maß für die
Reinheit des Materials. Für T
D ist ein Maß für die
Reinheit des Materials. Für T![]() 0 gilt
0 gilt ![]() D
D![]()
![]() und
und ![]() =
= ![]() D ist der Restwiderstand.
Auch das Restwiderstandsverhältnis (Residence Resistance Ratio)
D ist der Restwiderstand.
Auch das Restwiderstandsverhältnis (Residence Resistance Ratio) ![]() ist ein
Maß für die Reinheit. Für Metalle ist ein Wert von 10-3 typisch und für
Legierungen, amorphe Metalle ein Wert von
ist ein
Maß für die Reinheit. Für Metalle ist ein Wert von 10-3 typisch und für
Legierungen, amorphe Metalle ein Wert von ![]() 1. Hierbei ist der Phononenbeitrag
unwichtig.
1. Hierbei ist der Phononenbeitrag
unwichtig.
Die Temperaturabhängigkeit durch Phononenstreuung bei hohen Temperaturen
(T > ![]() ) ist lel - 1 = n .
) ist lel - 1 = n . ![]() Str, wobei n für die Phononenzustandsdichte steht,
welche proportional zu T ist.
Str, wobei n für die Phononenzustandsdichte steht,
welche proportional zu T ist. ![]() Str beschreibt den Streuquerschnitt bei der
Streuung an Debye-Phononen; diese Zahl ist temperaturunabhängig. Damit gilt
für die Leitfähigkeit
Str beschreibt den Streuquerschnitt bei der
Streuung an Debye-Phononen; diese Zahl ist temperaturunabhängig. Damit gilt
für die Leitfähigkeit ![]()
![]()
![]() G
G ![]() T-1 und
T-1 und ![]()
![]() T. Bei tieferen Temperaturen
(
T. Bei tieferen Temperaturen
(![]() 10K) liegt eine stärkere Temperaturabhängigkeit von nph und
10K) liegt eine stärkere Temperaturabhängigkeit von nph und ![]() Str vor, weil
Str vor, weil
![]() ph,dominant ~ T; das heißt, der Streuwinkel wird klein. Nach viel Rechenaufwand
erhält man:
ph,dominant ~ T; das heißt, der Streuwinkel wird klein. Nach viel Rechenaufwand
erhält man:
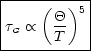
Diese Beziehung nennt man BLOCH-GRÜNEISEN-Gesetz.