8.5 QuantenHALLeffekt

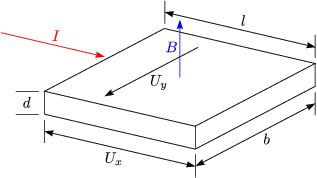
Betrachten wir folgende HALLgeometrie:

Im Gleichgewicht gilt j_y = 0. Der spezifische Widerstand in Längsrichtung lautet:

Für den Quer- und HALLwiderstand gilt _xy = .

8.5.1 Zweidimensionales Elektronengas (2 DEG)

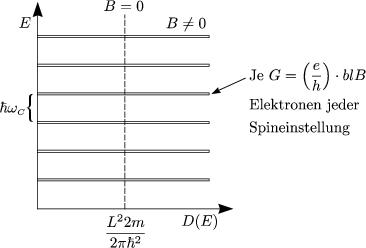
Falls ausschließlich volle LANDAUniveaus existieren, geht ; es ist keine Streuung möglich. Daraus folgt _xx0, aber auch E_x = 0 und damit _xx = = 0. j_x wird durch E_y getrieben, das heißt durch B. Es gibt ausschließlich volle LANDAUniveaus bei nd ^. b ^. l = ^. G, also bei B = nd. nd ist hierbei die Flächendichte und der sogenannte Füllfaktor. Bei _xx = 0 folgt der HALLwiderstand:

Experimentell wurde dieser Effekt von K.V.KLITZING beobachtet, welcher dafür den Nobelpreis erhielt. Bei der Meßkurve des HALLwiderstands sind sogenannte Hallwiderstand-Plateaus beobachtbar. Hier gilt zugleich _xx = 0 in breiten Banden! Die Idee ist nun folgende:

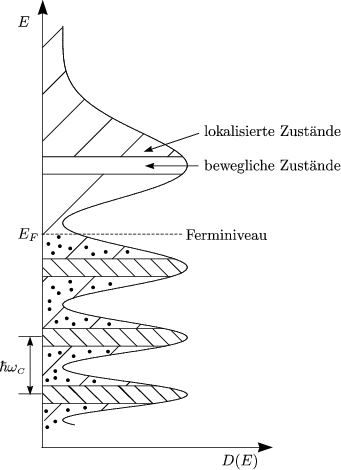
Das Ferminiveau wandert langsam durch lokalisierte Zustände, die selbst nicht zum Transport beitragen. Es gibt jedoch bis jetzt keine endgültige Erklärung für den Effekt. Eine Anwendung des Quantenhalleffekts ist das Eichnormal für .