2.8 Periodische Strukturen, Reziprokes Gitter

Wir haben eine dreidimensionale Streudichte (), welche periodisch in drei Dimensionen ist. Damit kann () durch eine Fourierreihe beschrieben werden.

h, k und l sind unabhängige ganze Zahlen. Für die Fourierkoeffizienten gilt:

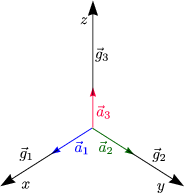
V _z ist die Periode der Funktion (), also die primitive Elementarzelle. Durch die Vektoren _hkl = h₁ + k₂ + l₃ und das schiefwinklige Koordinatensystem ₁, ₂, ₃ ist das sogenannte reziproke Gitter definiert. Die Wahl der Basisvektoren erfolgt so, daß im realen Raum Translationsinvarianz besteht, das heißt die Periodizität der Streudichte lautet:

Hierbei handelt es sich um das Gitter im realen Raum. Da _hkl ortsunabhängig (translationsinvariant) ist, folgt dann:

Also erhalten wir aus dieser Bedingung:

m ist hierbei eine ganze Zahl. Es gilt allgemein für beliebige h, k, l und n₁, n₂, n₃:

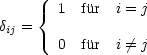
Die Konstruktionsvorschrift lautet:

Hierbei handelt es sich um die Elementarzelle des reziproken Gitters. Schließlich berechnen wir das Volumen dieser Elementarzelle im reziproken Raum:

Beispiele hierfür sind:

• Lineare Kette, Gitterkonstante a

  

  Das reziproke Gitter ist ebenfalls eine lineare Kette mit g = .

• Zweidimensional, schiefwinklig

  

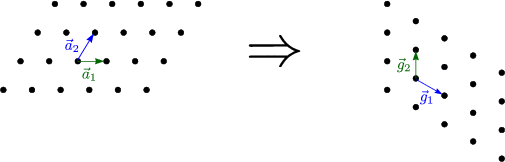
  ₂ und ₂ stehen senkrecht aufeinander.

• Kubisch primitiv

  

  

  Real		Reziprok
  fcc		bcc
  bcc		fcc

Zusammenhang zwischen reziprokem Gitter und Millerschen Indizes:

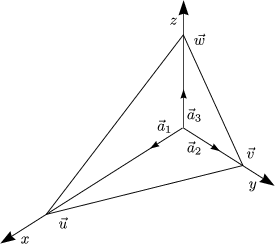
Es sei die Netzebene durch , , definiert. Bilde nun die Vektoren in der Netzebene, also beispielsweise -, , und davon das Kreuzprodukt. Daraus ergibt sich dann ein Vektor, welcher senkrecht auf der Ebene steht, also _hkl. Der Abstand berechnet sich nach:

Nochmal: _hkl sind die Wellenvektoren der Streudichte.