 . Wir wollen folgendes Gleichungssystem lösen:
. Wir wollen folgendes Gleichungssystem lösen:
Es gilt  . Wir wollen folgendes Gleichungssystem lösen:
. Wir wollen folgendes Gleichungssystem lösen:





Da Gleichungssystem besitzt also in  keine Lösung.
keine Lösung.  soll zu
soll zu  erweitert
werden
erweitert
werden  derart, daß:
derart, daß:
 lösbar ist: Eine Lösung wird durch i bezeichnet
lösbar ist: Eine Lösung wird durch i bezeichnet  .
.
 soll mit + und „
soll mit + und „ einen Körper bilden.
einen Körper bilden.
 - die schon bekannte
Multiplikation und Addition liefern.
- die schon bekannte
Multiplikation und Addition liefern.
Solch eine Erweiterung muß notwendig folgende Elemente enthalten:

In  wird wie im Reellen gerechnet, zu beachten ist zusätzlich
wird wie im Reellen gerechnet, zu beachten ist zusätzlich  .
.
 ,
, 
 ,
,  ,
,  ,
, 
 von
von  und
und  :
: 

Wir nehmen an,daß  . Dann folgt daraus für i:
. Dann folgt daraus für i:

Die imaginäre Einheit i wäre also im Zahlenbereich  der reellen Zahlen, was
ein Widerspruch darstellt. Daraus ergibt sich also:
der reellen Zahlen, was
ein Widerspruch darstellt. Daraus ergibt sich also:

 sind eindeutig
sind eindeutig  und
und  mit
mit  zugeordnet. Hier liegt also
eine beliebige Zuordnung zwischen
zugeordnet. Hier liegt also
eine beliebige Zuordnung zwischen  und
und  vor.
vor.

Es seien  und
und  mit
mit  ,
,  ,
,  ,
,  . Dann wird Addition
und Multiplikation folgendermaßen definiert:
. Dann wird Addition
und Multiplikation folgendermaßen definiert:
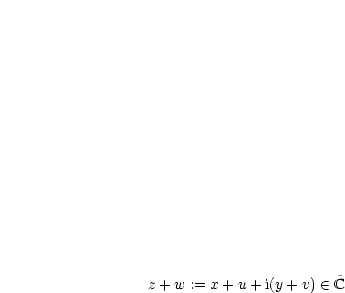



 ist neutral bezüglich der Addition:
ist neutral bezüglich der Addition: 
 ist invers zu
ist invers zu  bezüglich der Addition:
bezüglich der Addition:


 ist abelsche Gruppe.
ist abelsche Gruppe.
 ist neutral bezüglich der Multiplikation:
ist neutral bezüglich der Multiplikation:  .
.
 ,
,  hierzu bezüglich der Multiplikation ist
hierzu bezüglich der Multiplikation ist
 invers zu
invers zu 
 ist eine abelsche Gruppe.
ist eine abelsche Gruppe.

 ist abelsche Gruppe.
ist abelsche Gruppe.
 ,
, ,
, :
:  .
.
 ist ein Körper, der die Forderungen 1./2. erfüllt.
ist ein Körper, der die Forderungen 1./2. erfüllt.
 ist der Körper der komplexen Zahlen.
ist der Körper der komplexen Zahlen.
 einer komplexen Zahl ist festgelegt durch:
einer komplexen Zahl ist festgelegt durch:

Der Betrag von  ist der Abstand von
ist der Abstand von  zum Ursprung
zum Ursprung  der
Gaußschen Zahlenebene.
der
Gaußschen Zahlenebene.


 ist
ist  gespiegelt an der reellen Achse.
gespiegelt an der reellen Achse.

 und
und  folgt:
folgt:













 ,
,  ,
, 
Im Reellen gilt  , aber im Komplexen ist im allgemeinen
, aber im Komplexen ist im allgemeinen
 .
.
 :
: 

|
|
 ist der Abstand zwischen
ist der Abstand zwischen  und
und  . Es sei
. Es sei  :
:
 mit
mit  : Kreis um
: Kreis um  mit
Radius 3
mit
Radius 3
 mit
mit  : Inneres des obigen
Kreises
: Inneres des obigen
Kreises
 mit
mit  : Äußeres des obigen
Kreises
: Äußeres des obigen
Kreises
Betrachten wir folgendes Beispiel: Was bedeutet  geometrisch?
geometrisch?



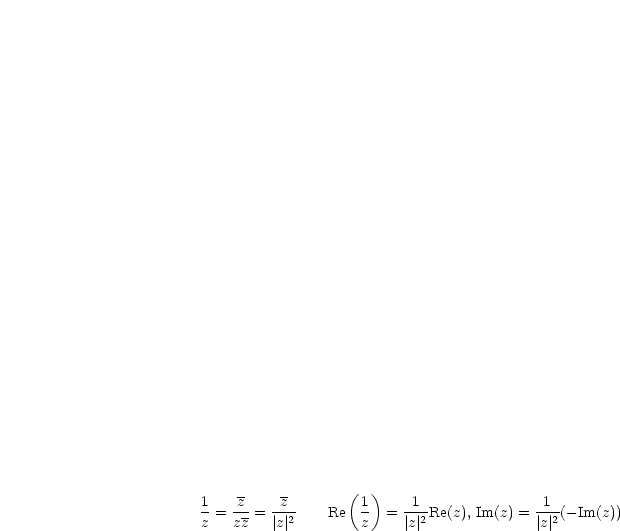










 wird zur positiven reellen Achse gerechnet.
wird zur positiven reellen Achse gerechnet.
|
Es sei |
|
Jede komplexe Zahl  kann in der Form
kann in der Form  dargestellt
werden, wobei
dargestellt
werden, wobei  und
und  ist.
ist.
Es sei  und
und  gegeben. Dann
gilt:
gegeben. Dann
gilt:


Insbesondere gilt:



|
|
Vorausgesetzt werden:








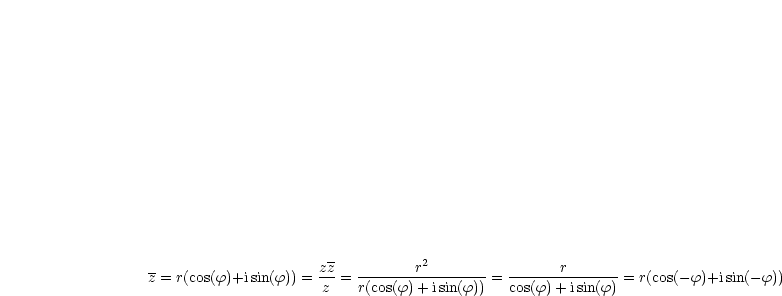





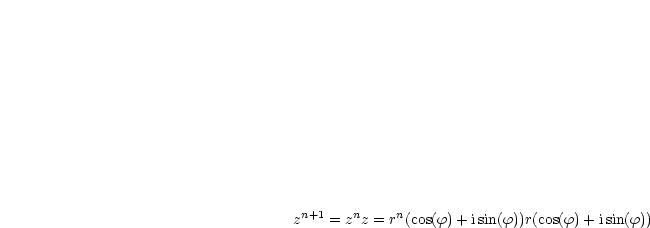
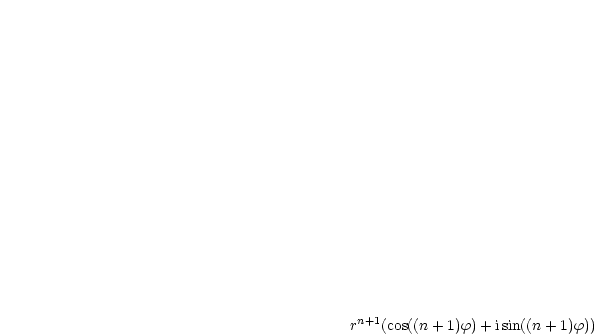
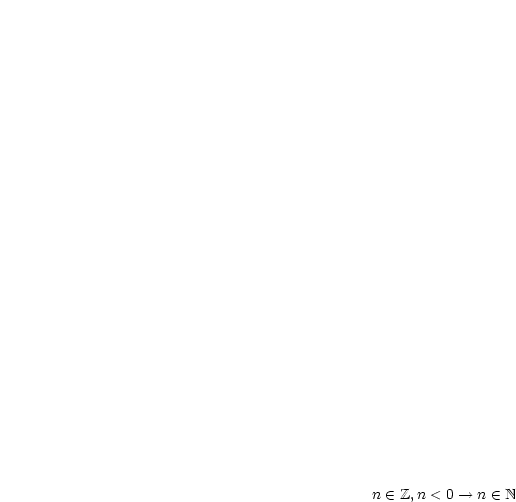
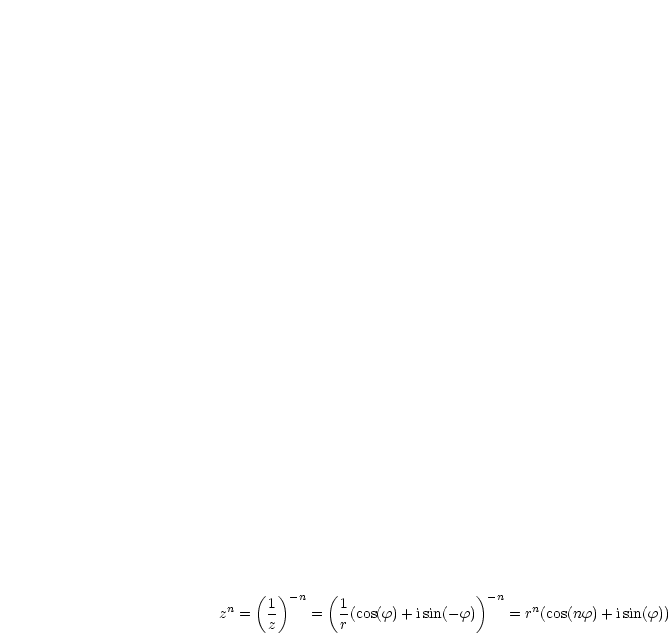
Es ist  zu konstruieren (ähnliche Dreiecke).
zu konstruieren (ähnliche Dreiecke).
Gegeben sei  ,
,  . Gesucht sind alle
. Gesucht sind alle  mit
mit  . Jede Lösung
dieser Gleichung heißt
. Jede Lösung
dieser Gleichung heißt  -te Wurzel aus
-te Wurzel aus  .
.

 und
und  sind gesucht!
sind gesucht!

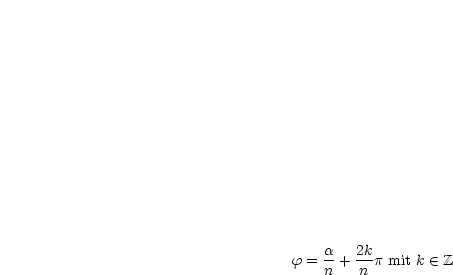
|
Es seien |
|
|
|
|
Es sei |
Die Zahlen |
|


Dies sind die  -ten Einheitswurzeln der Zahl 1.
-ten Einheitswurzeln der Zahl 1.
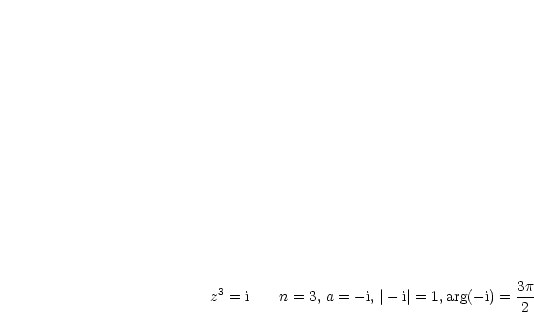
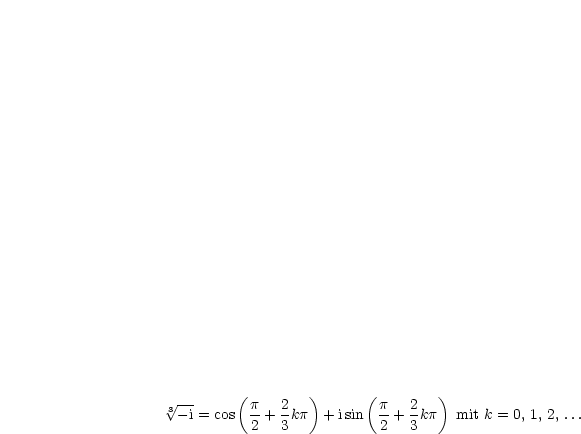
| z2 + 2az + b | = 0 (a,b,  ) ) | ||
| z2 + 2az + a2 | = a2 - b | ||
| (z + a)2 | = a2 - b | ||
| z | = -a +  | ||



Verboten sind Ungleichungen zwischen komplexen Zahlen!