3.1 Komposition (Hintereinanderausführung) von Abbildungen
3.2 Der Funktionsbegriff
3.2.1 Gleichheit von Funktionen
3.2.2 Komposition von Funktionen
3.3 Surjektivität und Injektivität
3.3.1 Monotonie von Funktionen
3.4 Reelle Zahlen
3.4.1 Die Gruppe
3.4.2 Axiomensystem für die reellen Zahlen
3.4.3 Körperaxiome
3.4.4 Anordnungsaxiome
3.5 Vollständigkeitsaxiom
3.6 Rechnen mit Maxima/Minima
3.7 Vollständige Induktion Fakultät, Binomialkoeffizient
3.7.1 Induktionssatz
3.7.2 Beweisschema Vollständige Induktion
3.7.3 Definition durch Induktion/Rekursive Definition
3.7.4 BERNOULLIsche Ungleichung
3.7.5 Geometrische Summe
3.7.6 Binomialkoeffizient
3.8 Der binomische Satz
3.8.1 PASCALsches Dreieck
3.9 Betrag einer reellen Zahl/Ungleichungen
3.9.1 Vorzeichenfunktion
3.9.2 Betragsfunktion
3.9.3 Ungleichung zwischen dem geometrischen und arithmetischen Mittel (GAM-Ungleichung)
3.10 CAUCHY-SCHWARZsche Ungleichung
3.11 Komplexe Zahlen
3.11.1 Definition von Addition und Multiplikation in
3.11.2 Polardarstellung komplexer Zahlen
seien Mengen. Eine 
in 
ist eine Vorschrift, die jedem 
eindeutig ein 
zuordnet. Folgende Schreibweisen sind dabei üblich:
: 
: 
heißt 
in 
, 
heißt 
von 
, 
heißt
. Die Menge 
es gibt 
mit 
heißt 
. 
nennt man 
heißt 
. Die Urbildmenge ist 
. 
: 
ist eine Funktion, falls aus 
folgt: 
(
. Eine äquivalente Formulierung wäre: Aus 
folgt
.
: 
sei eine Funktion: graph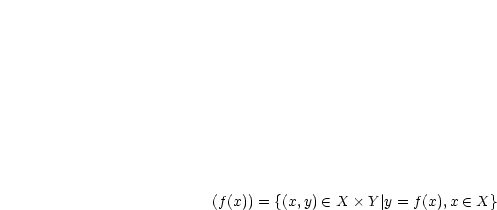
.