

Es sei die Funktion  als sogenannte Betragsfunktion definiert. Für
die gibt es verschiedene Schreibweisen:
als sogenannte Betragsfunktion definiert. Für
die gibt es verschiedene Schreibweisen:

Des weiteren gelten folgende Beziehungen:



|
Es seien
|




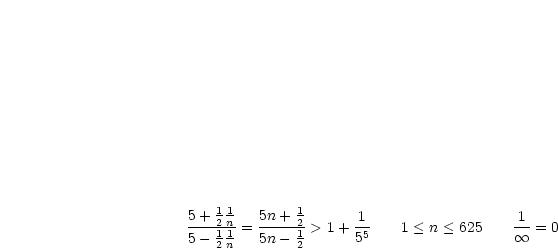


|
Es seien
|
Wir verwenden für den ersten Teil einen Trick:




Weiterhin folgt:

Daraus ergibt sich nun der zweite Teil der Ungleichung:

Es sei  ,
,  ,
,  ,
,  :
:

Für  folgt die Identität
folgt die Identität  . Diese Aussage ist wohl wahr.
. Diese Aussage ist wohl wahr.
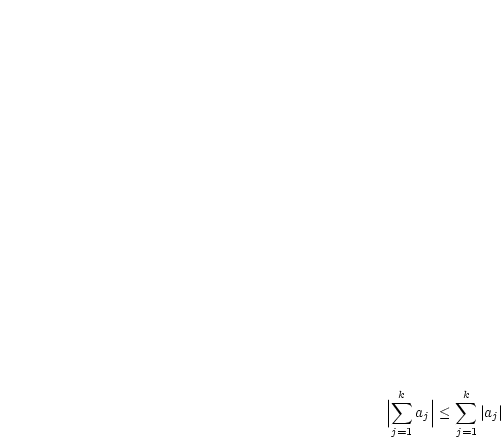

Durch Anwenden der Dreiecksungleichung ergibt sich schließlich:


Für  ,
,  gilt
gilt  .
.
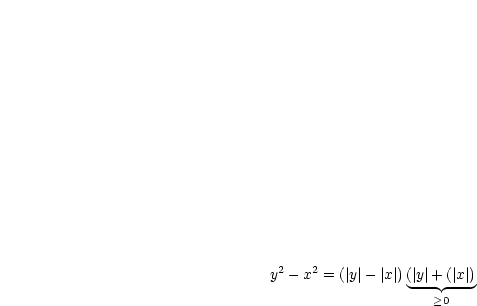
Gegeben sind  und
und  . Für welche
. Für welche  gilt
gilt 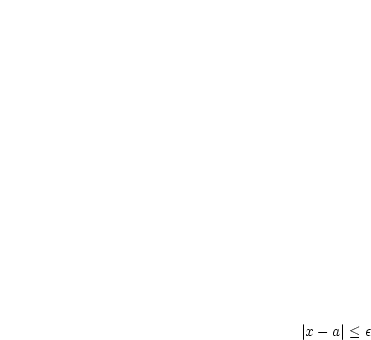 ?
?


Daraus folgt dann:



Quadriere die Ungleichung 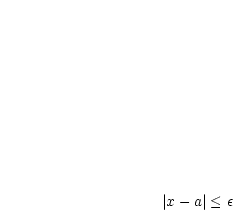 :
: 
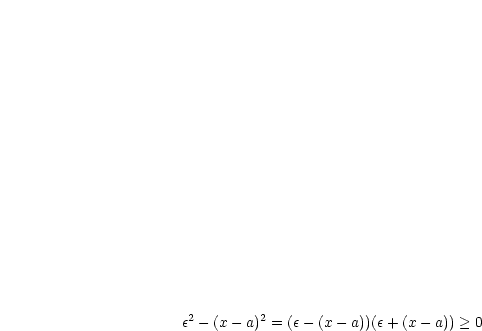
 und
und 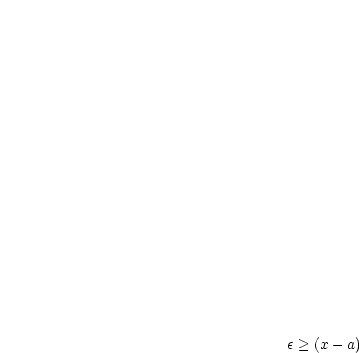

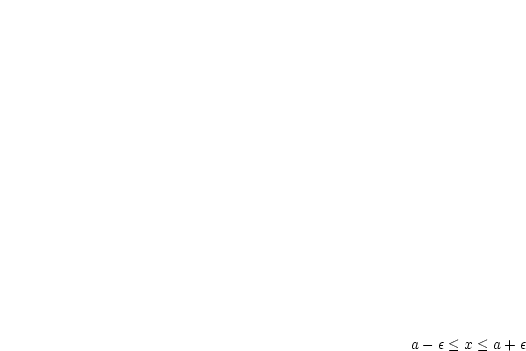
 und
und  Dies ist unmöglich!
Dies ist unmöglich!
Gegeben sind  und und  . Dann gilt: . Dann gilt: |
 |