,
,  ,
,  ,
,  ,
,  ,
,  ,
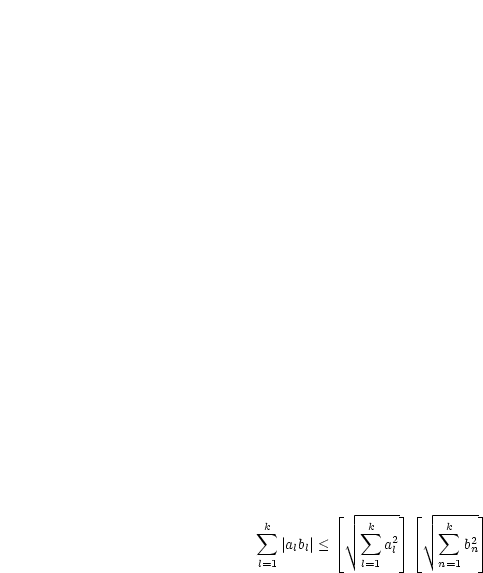
,  . Dann gilt die
CAUCHY-SCHWARZsche Ungleichung:
. Dann gilt die
CAUCHY-SCHWARZsche Ungleichung:
Gegeben sind  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . Dann gilt die
CAUCHY-SCHWARZsche Ungleichung:
. Dann gilt die
CAUCHY-SCHWARZsche Ungleichung:

Wir können schreiben:  für
für  und
und  . Aus
. Aus
 oder
oder  folgt
folgt 

 oder
oder 

 . In diesem
Fall ist nichts zu beweisen. Wir ziehen die Konstanten
. In diesem
Fall ist nichts zu beweisen. Wir ziehen die Konstanten  und
und  in die
Summe:
in die
Summe:

Es gilt die Dreiecksungleichung:

Außerdem gilt folgende Abschätzung:

Mit diesen Erkenntnissen folgt nun mit  und
und  :
:
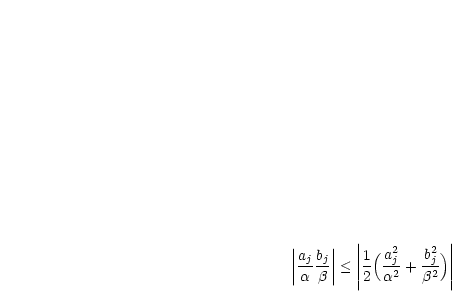
Wir summieren diese Ausdrücke auf und erhalten:

Für  ,
,  ,
,  ,
,  ,
,  ,
,  :
: