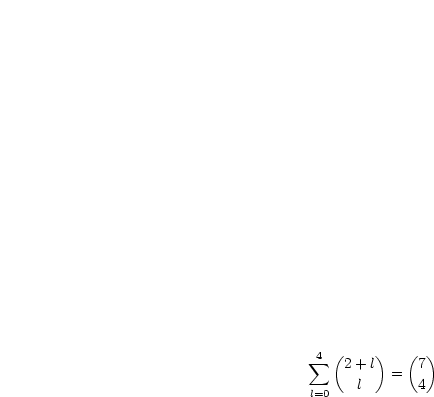Es sei  , ,  . Dann gilt folgende Beziehung: . Dann gilt folgende Beziehung: |
 mit mit ![[( ) ( ) ( )]
n n n+ 1
k- 1 + k = k](ma1048x.gif) |
Es sei  , ,  . Dann gilt folgende Beziehung: . Dann gilt folgende Beziehung: |
 mit mit ![[( ) ( ) ( )]
n n n+ 1
k- 1 + k = k](ma1048x.gif) |

Für  gilt:
gilt:

Es sei  ,
,  . Setze oben
. Setze oben  :
:

Wir multiplizieren mit  durch und erhalten:
durch und erhalten:

Dann kann die Gleichung noch folgendermaßen umgeformt werden, wobei folgt:
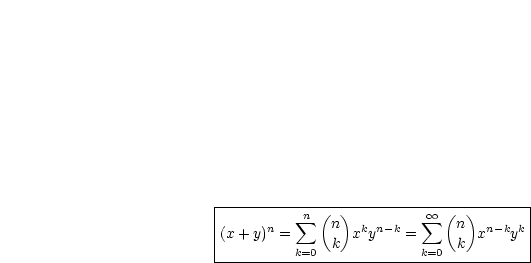
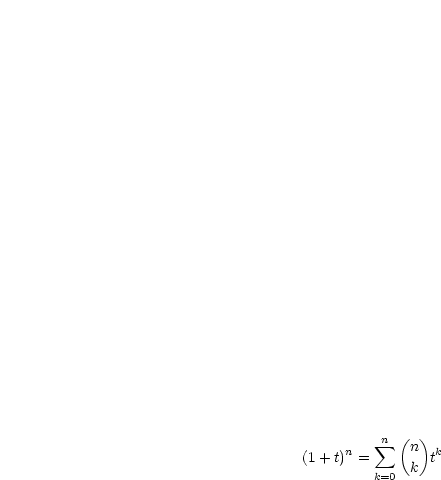
 :
:

 :
:

Wir addieren die Ausdrücke  und
und  :
:

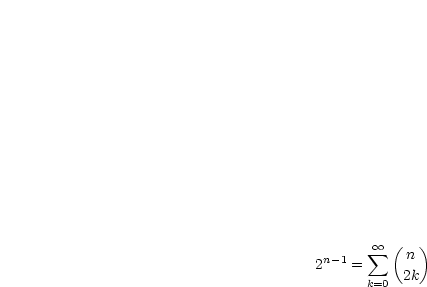
Die Ausdrücke  und
und  werden subtrahiert:
werden subtrahiert:
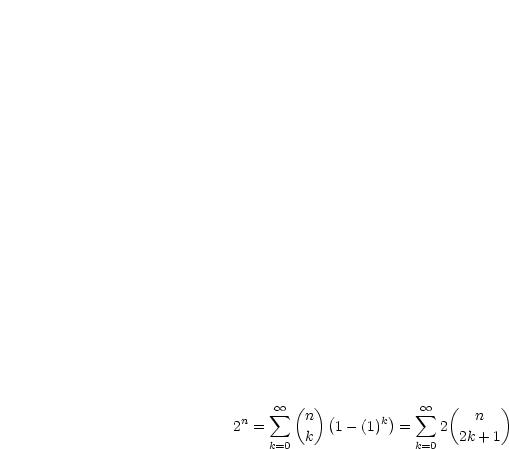
Es sei zu zeigen, daß für  ,
,  gilt:
gilt:


Nun notieren wir uns das Pascalsche Dreieck:



Es gilt, wie wir zeigen sollten:

Für  ,
,  folgt durch Einsetzen:
folgt durch Einsetzen:

Weiterhin gilt:

Auch hier folgt für  ,
,  durch Einsetzen:
durch Einsetzen: