3.7 Vollstndige Induktion Fakultt, Binomialkoeffizient

3.7 Vollständige Induktion Fakultät, Binomialkoeffizient

Zunächst führen wir folgende nützliche Schreibweisen für die Summe und das Produkt ein. Im folgenden werden nur noch diese abkürzenden Schreibweisen verwendet, deshalb ist es wichtig, diese zu verstehen:

Produkt: $prod n a1, a2, a3, ..., ak, ...: a1 .a2 .a3 .....an = aj j=1$
Summe: $sum n a1, a2, a3, ..., ak, ...: a1 + a2 + ...+ an = al l=1$

Definition:

$M (_ R$ heißt induktiv, falls erfüllt sind:

$1 (- M$
Aus $x (- M$ folgt: $x + 1 (- M$

R, Q,Z besitzen diese Eigenschaft.

$N$ , die Menge der natürlichen Zahlen, ist die kleinste induktive Teilmenge von $R$ .

3.7.1 Induktionssatz

Ist $M$ eine induktive Teilmenge der natürlichen Zahlen, so gilt: $M = N$ .

Begründung:

Gilt $N < M < N$ , so ist $M = N$ . Das heißt, gelten für $M < N$ :

$1 (- M$
Aus $n (- M$ folgt $n+ 1 (- M$

$==>$ Dann hat man $M = N$ .

3.7.2 Beweisschema Vollständige Induktion

$A(n)$ sei eine Aussage, die von $n (- N$ abhängt. Das Ziel ist es, zu zeigen, daß $A(n)$ richtig ist $A$ $n$ $(- N$ . Folgende Aussagen können beispielsweise über vollständige Induktion überprüft werden:

$2n +1$ ist ungerade $A$ $n (- N$ .
$2 n - n + 41$ ist $A$ $n$ eine Primzahl.
$sum n n k = -(n + 1) k=1 2$

1.Schritt: Induktionsanfang
Man zeige, daß $A(1)$ richtig ist.
2.Schritt: Induktionsschluß
- Induktionsvoraussetzung:
  Man nimmt an, daß $A(k)$ richtig ist für beliebige $k (- N$ .
- Induktionsbedingung:
  Dann folgt daraus, daß $A(k + 1)$ richtig ist.

Wenn dies gezeigt ist, dann ist $A(n)$ $A$ $n$ $(- N$ richtig. $M$ sei folgende Menge:

|--------------------------| -M--=-{n (- -N-|A(n)-ist richtig.}

Da Element 1 befindet sich dann in $M$ : $1 (- M$ . Dann folgt natürlich aus $k (- N$ , daß $k+ 1 (- M$ . Es kann auch sein, daß die Aussage erst ab einem bestimmen $n0 > 1$ gilt, wie beispielsweise hier:

2n > n2 f¨ur n > 5

Dann muß man betrachten:

M (n) = A(n +n0 - 1) f¨ur n = 1,2,...

Induktionsvoraussetzung:
Es sei $k > n0$ beliebig und $A(m)$ sei richtig für $n0 < m < k$ .
Induktionsbehauptung:
Dann ist $A(k+ 1)$ richtig.

Das Ergebnis ist, daß $A(n)$ für $n > n0$ stimmt. Bei manchen der folgenden Beispiele fehlen die Induktionsanfänge; diese können als Übung vervollständigt werden.

Beispiel:

Es sei zu beweisen:

|-n--------------------------| | sum k = n(n +1) fur n = 1,2,... |k=1 2 ¨ | -----------------------------

Induktionsanfang:
Für $n = 1$ gilt:
$sum 1 1 k = 2(1+ 1) = 1 k=1$
Die linke und rechte Seite der Gleichung stimmen somit überein. Damit ist $A(n)$ für $n = 1$ gezeigt.
Induktionsschluß:
- Induktionsvoraussetzung:
  Wir wählen $k (- N$ beliebig und setzen voraus:
  $sum k k- j = 2 (k + 1) j=1$
- Induktionsbehauptung: $k sum +1 k+ 1 j = -2--(k +2) j=1$
Mittels der Induktionsvoraussetzung können wir nun die Gleichung beweisen:
$k sum +1 sum k k k + 2 j = +k + 1 = 2(k +1) +k + 1 = (k +1)-2-- j=1 j=1$

Beispiel:

Es sei zu beweisen:

| sum n-(--)------------------| | k n = n .2n-1 f¨ur n (- N| |k=0 k | ---------------------------

Induktionsanfang:
Für $n = 1$ gilt:
$sum 1 ( ) k n = 0+ 1 = 1 k=0 k$

$1- 1 0 1 .2 = 1.2 = 1$
Die linke und rechte Seite der Gleichung stimmen somit überein. Damit ist $A(n)$ für $n = 1$ gezeigt.
Induktionsschluß:
- Induktionsvoraussetzung:
  Wir wählen $k (- N$ beliebig und setzen voraus:
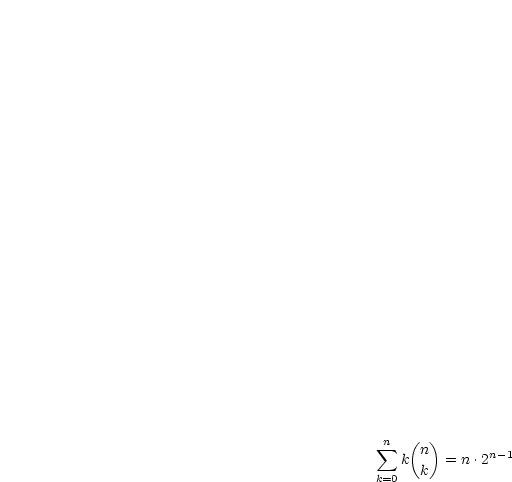
  $n ( ) sum k n = n.2n-1 k=0 k$
- Induktionsbehauptung: $n+1 ( ) sum n+ 1 n k k = (n+ 1).2 k=0$
Mittels der Induktionsvoraussetzung können wir nun die Gleichung beweisen:
$( ) ( ) n+ sum 1 n + 1 n sum n + 1 S = k k = k k + (n +1) k=0 k=0$
Es gilt die Beziehung:
$|------------------------| |(n) ( n ) (n + 1) | | k + k + 1 = k + 1 | -------------------------$
Damit ergibt sich nun:
$( ) ( ) [( ) ( )] sum n n+ 1 n sum n + 1 sum n n n S = k k + (n+ 1) = k k + (n +1) = k k- 1 + k + (n+ 1) = k=n0 ( ) n ( )k=0 n-1 ( )k=0 n ( ) sum n sum n sum n sum n = k k- 1 + k k + (n + 1) = (k + 1) k + k k + (n +1) = k=n1 ( ) k=0 n ( ) k=0 n ( k=)0 n ( ) n ( ) = sum (k+ 1) n - (n +1) + sum k n + (n+ 1) = sum k n + sum n + sum k n = k=0 k k=0 k k=0 k k=0 k k=0 k sum n ( ) sum n ( ) ( ) |--------| = 2 . k n + n IV= 2. n .2n-1 + 2n = n .2n + 2n = 2n (n + 1)| k=0 k k=0 k ----------$ (3.1)

Beispiel:

Es sei zu beweisen:

|----------------------------| | sum n 1 1 | | k2 +-k-= 1- n-+-1 f¨ur n (- N -k=1---------------------------

Induktionsanfang:
Für $n = 1$ gilt:
$sum 1 1 1 1 k2-+-k = 12 +-1 = 2 k=1$

$1- --1--= 1 - 1 = 1 1 + 1 2 2$
Die linke und rechte Seite der Gleichung stimmen somit überein. Damit ist $A(n)$ für $n = 1$ gezeigt.
Induktionsschluß:
- Induktionsvoraussetzung:
  Wir wählen $k (- N$ beliebig und setzen voraus:
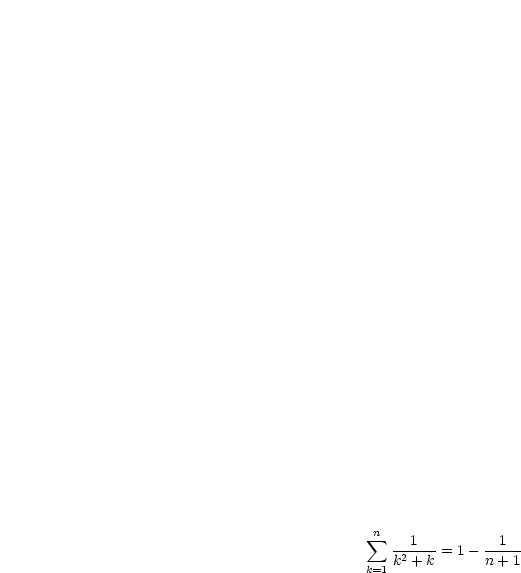
  $n sum --1---= 1 - -1--- k=1k2 + k n+ 1$
- Induktionsbehauptung: $n sum +1 1 1 k2-+k-= 1 - n+-2- k=1$
Dann ergibt sich durch Transformation der Summation:
$n+ sum 1 --1--- sum n--1--- -------1------- IV --1-- -------1------- k2 + k = k2 + k + (n + 1)2 +(n + 1)= 1 - n+ 1 + (n+ 1)2 + (n+ 1) = k=1 k=1 2 2 = 1- -1---+ ----1-----= (n--+3n-+-2)--(n+-2)+-1 = n--+2n-+-1 = n+ 1 n2 + 3n +2 n3 + 3n + 2 n2 +3n + 2 n2-+-3n+-2--(n-+1) n2-+3n-+-2 --n-+-1--- --n-+-1--- = n2 + 3n+ 2 = n2 +3n + 2 - n2 + 3n +2 = 1 - n2 + 3n+ 2 = n + 1 |-----1--| = 1- (n-+-1)(n-+-2) =|1- n-+-2| ----------$ (3.2)

Beispiel:

Es sei zu beweisen:

|--------------------------------------------| | sum n x2i- 1 1 1 | | -----2i = ------ -----2n-f¨ur n (- N und x /= 1 -i=11---x----1--x---1---x--------------------

Induktionsanfang:
Für $n = 1$ gilt: Die linke und rechte Seite der Gleichung stimmen somit überein. Damit ist $A(n)$ für $n = 1$ gezeigt.
Induktionsschluß:
- Induktionsvoraussetzung:
  Wir wählen $i (- N$ beliebig und setzen voraus:
  $n i- 1 sum -x2--- = --1--- ---1--- i=1 1- x2i 1- x 1- x2n$
- Induktionsbehauptung: $sum n x2i- 1 1 1 1---x2i = 1--x-- 1---x2n+1 i=1$
Dann ergibt sich durch Transformation der Summation:
$n sum +1 2i-1 sum n 2i-1 2n 2n S = -x---i = x----i +---x-n+1 IV= --1--- ---1--n +---x--n+1 = i=1 1- x2 i=1 1- x2 1 - x2 1 - x 1 - x2 1 - x2 1 1- x2n+1- x2n (1- x2n) 1 1- x2n+1- x2n +x2.2n = ------ -------2n--(----2n+1)---= ------ ----2n+1---2n----3.2n-= 1- x (1 - x )1 - x ( 1- x 1-)x - x +x -1--- 1--x2n+1--x2n +-x3.2n-+-x2.2n---x3.2n -1--- ----x3.2n--x2.2n---- = 1- x - 1- x2n+1- x2n + x3.2n = 1- x - 1+ (1- x2n)(1- x2n+1)= 2.2n ( 2n) 2.2n 2.2n 2.2n = -1---- 1+ ---x----(1--x----)= -1----1 - --x--n+1 = -1---+ x-----1--n+x1---= 1- x (1- x2n) 1- x2n+1 1- x 1- x2 1- x 1- x2 |--1--------1----| = |1---x- -----2n+1 | --------1---x----|$ (3.3)

Beispiel:

Man zeige, daß gilt:

|---------------| 2n > n2 f¨ur n > 5 -----------------

Induktionsanfang: $25 = 32 > 52 = 25$
Die Aussage stimmt.
Induktionsschluß:
- Induktionsvoraussetzung:
  Wir wählen $k > 5$ beliebig und setzen voraus:
  $k 2 2 > k$
- Induktionsbehauptung: $2k+1 > (k + 1)2$
Für $k > 5$ folgt:
$k- 1 > 5 ==> (k - 1)2 = k2- 2x+ 1 > 25 ==> k2 > 2k+ 24 > 2k+ 1$
Damit ergibt sich nun die zu zeigende Beziehung:
$2k+1 = 2.2k > 2k2 = k2 + k2 > k2 + 2k+ 1 = (k + 1)2$

Beispiel:

Man zeige, daß gilt:

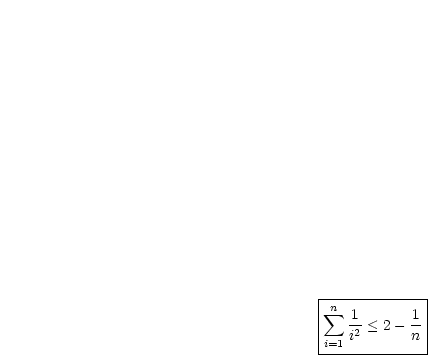
|------------| sum n 1 1| | 2-< 2- --| -i=1-i------n--

Induktionsanfang: $sum 1 1 1- i2 = 12 = 1 i=1$

$2 - 1 = 1 1$

$1 = 1$
Die Aussage stimmt somit.
Induktionsschluß:
- Induktionsvoraussetzung:
  Wir wählen $k > 1$ beliebig und setzen voraus:
  $n sum 1-< 2- -1 i=1 i2 n$
- Induktionsbehauptung: $n sum +11 1 -2 < 2 ------ i=1 i n+ 1$
$n sum +1 sum n IV S = 12-= -12+ ---1--2< 2- 1-+---1--2 = 2--1+ -2--1-----< 2- 1+ -21--- i=1 i i=1i (n+ 1) n (n +1) n n + 2n+ 1 n n + n$
Mittels Partialbruchzerlegung ergibt sich:
$1 1 1 -2----= --- ----- n + n n n + 1$
Dann folgt durch Einsetzen:
$|--------| 2- 1-+ --1---= 2 - 1-+ 1- -1---= 2 - --1--| n n2 + n n n n+ 1 ----n-+1--$
Damit folgt also die Behauptung, womit die Ungleichung stimmt.

Beispiel:

Man zeige, daß gilt:

|n-------2------2| sum i3 = n-(n+-1)-| |i=1 4 | ------------------

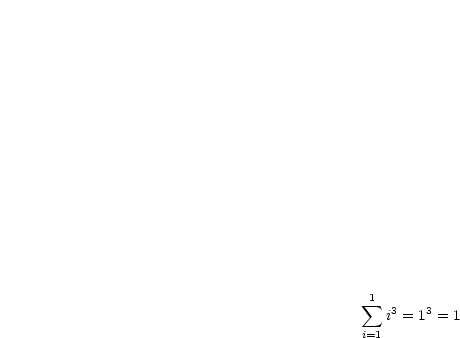
Induktionsanfang: $1 sum 3 3 i=1i = 1 = 1$

$12 .22 --4-- = 1$
Die Aussage stimmt somit.
Induktionsschluß:
- Induktionsvoraussetzung:
  Wir wählen $k > 1$ beliebig und setzen voraus:
  $sum n n2(n+ 1)2 i3 = --------- i=1 4$
- Induktionsbehauptung: $n sum +1 3 (n-+-1)2(n-+2)2 i = 4 i=1$
$n sum +1 sum n 2 2 2[ ] S = i3 = i3 + (n + 1)3 IV= n-(n-+1)- + (n + 1)3 = (n+-1)- n2 + 4(n + 1) = i=1 i=1 4 4 2 [ ] 2 |-----2------2-| = (n-+-1)- n2 + 4n +4 = (n+-1)-(n +2)2 = (n-+-1)(n+-2)- | 4 4 -------4--------$ (3.4)

Beispiel:

Man zeige, daß gilt:

|----------------------| | 2 sum n-1 | |n-< 1-< n f¨ur n > 2| |2 k=1 k | -----------------------

Induktionsanfang: Die Aussage stimmt.
Induktionsschluß:
- Induktionsvoraussetzung:
  Wir wählen $k > 2$ beliebig und setzen voraus:
  $2n-1 n-< sum 1-< n 2 k=1 k$
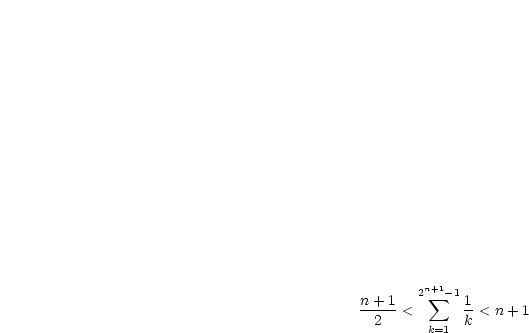
- Induktionsbehauptung: $2n+ sum 1-1 n-+-1< 1-< n+ 1 2 k=1 k$
Wir zeigen zuerst die linke Ungleichung:
$n+1 n n n n n n n n n 2 sum -11 2 + sum 2 -11 2 sum -11 2+2 sum -1 1IV n 2+2 sum -1 1 n 2 + sum 2 -1 1 k-= k-= k-+ k-> 2-+ k-> 2-+ 2n+1-= k=1 k=1 k=1 |--k=2n k=2n k=2n n- n -1--- |n+-1-| = 2 + 2 .2.2n = --2----$ (3.5)

Außerdem gilt für die rechte Ungleichung:
$2n+1-1 2n+2n-1 2n-1 2n+2n-1 2n+2n-1 2n+2n-1 sum 1-= sum 1-= sum 1-+ sum 1-IV< n+ sum 1-< n+ sum -1 = n+2n.1- = |n+-1-| k=1 k k=1 k k=1 k k=2n k k=2n k k=2n 2n 2n ------|$
Damit ist die Ungleichungskette bewiesen.

Beispiel:

Man zeige, daß gilt:

|------------------| |(a + b)n an + bn| | --2-- < ---2---| -------------------

Induktionsanfang: Die Aussage stimmt.
Induktionsschluß:
- Induktionsvoraussetzung:
  Wir wählen $k > 2$ beliebig und setzen voraus:
  $(a + b)n an + bn ----- < ------- 2 2$
- Induktionsbehauptung: $(a + b)n+1 an+1 + bn+1 --2-- < -----2-----$
$( ) ( ) ( ) a-+-b n+1 a-+b- n a+-b- IV an +-bn a+-b- an+1 +-abn +-ban-+-bn+1 2 = 2 . 2 < 2 . 2 = 4 = an+1 + bn+1 abn + ban an+1 + bn+1 an+1 + bn+1 abn + ban = ----4-----+ ---4----= ----2------ -----4-----+ ----4----= n+1 n+1 ( ) = a---+-b---+ 1 abn + ban- an+1 - bn+1 = 2 4 |-----------| = an+1 +-bn+1+ 1(bn- an)(a- b)< |an+1 +-bn+1| 2 4 ----- ----- -----2------| <0$ (3.6)

Beispiel:

Man zeige, daß gilt:

|------------------------| | prod n prod n | | (n+ k) = 2n (2k - 1) | -k=1-----------k=1-------

Induktionsanfang: Die Aussage stimmt.
Induktionsschluß:
- Induktionsvoraussetzung:
  Wir wählen $n > 1$ beliebig und setzen voraus:
  $prod n prod n (n+ k) = 2n (2k -1) k=1 k=1$
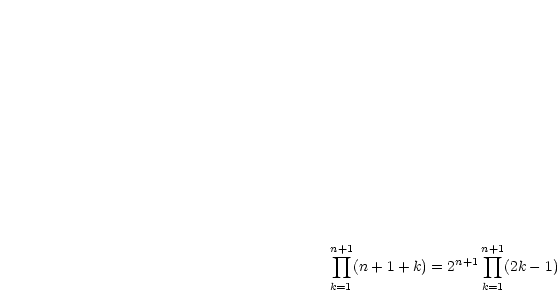
- Induktionsbehauptung: $n+ prod 1 n+1n prod +1 (n+ 1 + k) = 2 (2k- 1) k=1 k=1$
Nun folgt durch Transformation des Summationsindex:
$n+1 n+2 n+2 n prod (n + k+ 1) = prod (n+ k) = prod (n + k).-1-= prod (n+ k)(2n-+1)(2n+-2) IV= k=1 k=2 k=1 n + 1 k=1 n +1 n n+1 = 2n prod (2k- 1) .(2n-+-1).2.(n-+1)-= 2n prod (2k- 1).2 .2n+-1-= k=1 n+ 1 k=1 2n+ 1 n- 1 |----n+1-------| n prod | n+1 prod | = 2 (2k - 1) .2 =|2 (2k- 1)| k=1 -----k=1--------$ (3.7)

Beispiel:

Man zeige schließlich noch die Ungleichung zwischen dem geometrischen und arithmetischen Mittel:

|----------------| | prod n sum n | |n V~ ai < 1 ai| | i=1 n i=1 | ------------------

Induktionsanfang: Die Aussage stimmt.
Induktionsschluß:
- Induktionsvoraussetzung:
  Wir wählen $k > 1$ beliebig und setzen voraus:
  $2k--- 2k 2k V~ prod ai <-1 sum ai i=1 2k i=1$
- Induktionsbehauptung: $2k+1--- 2k+1 2k+1 V~ prod a < --1- sum a i=1 i 2k+1 i=1 i$
Induktionsbeweis:
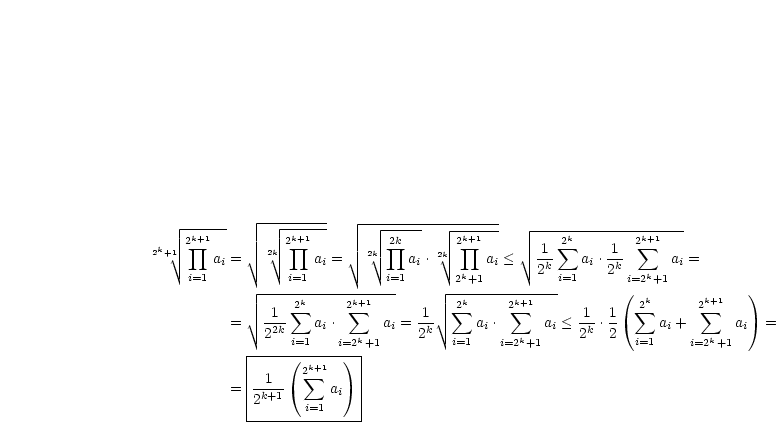$--------- ------------------ 2k+1--- 2k+1--- -2k-- 2k+1--- ---2k-------2k+1--- 2k+ V~ 1 prod a = V~ 2k V~ prod a = V~ 2 V~ k prod a .2k V~ prod a < V~ -1 sum a .1- sum a = i=1 i i=1 i i=1 i 2k+1 i 2k i=1 i 2ki=2k+1 i ----------------- -------------- ( ) 1 sum 2k 2k sum +1 1 sum 2k 2k sum +1 1 1 sum 2k 2k sum +1 = V~ 22k ai . ai = 2k V~ ai . ai < 2k .2 ai + ai = i=1 i=2k+1 i=1 i=2k+1 i=1 i=2k+1 |----(2k+1--)-| |-1-- sum | = |2k+1 i=1 ai | ---------------$ (3.8)

Nun haben wir die Ungleichung für beliebige Zweierpotenzen gezeigt. Nun zeigen wir außerdem, daß $A(n) '--> A(n -1)$ .
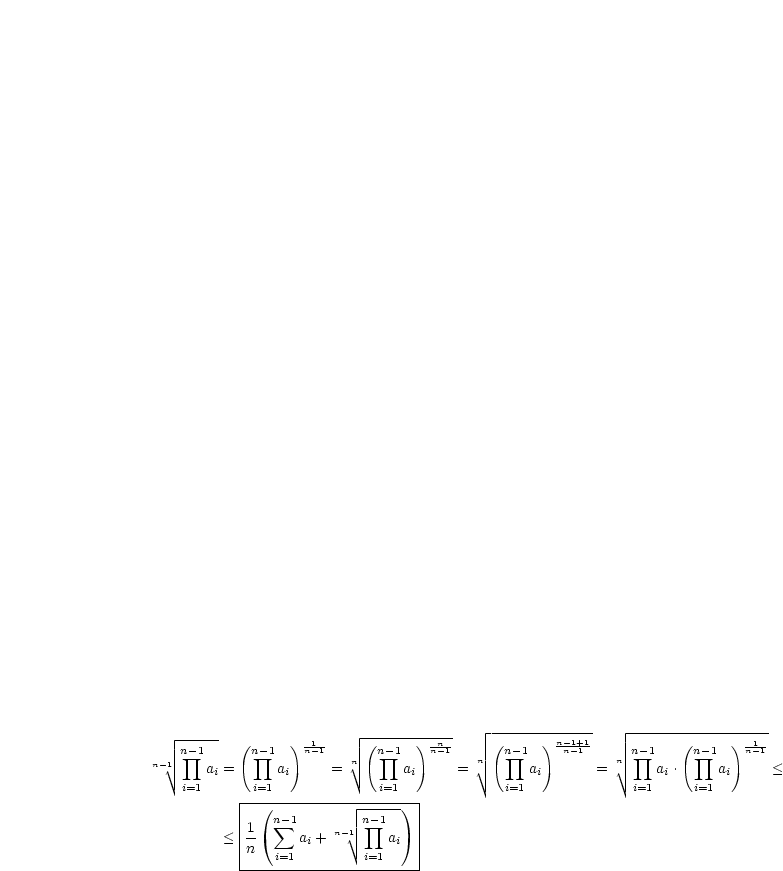$----------- ------------- ------------------ n--1-- (n- 1 ) n1-1 (n-1 ) nn-1 (n-1 ) n-n 1-+11 n-1 (n -1 )n1-1 n-1 V~ prod ai = prod ai = n V~ prod ai = n V~ prod ai = n V~ prod ai . prod ai < i=1 i=1 i=1 i=1 i=1 i=1 |-(-----------------)-| | n sum -1 n- prod 1 | < |1- ai + n- V~ 1 ai | |n i=1 i=1 | -----------------------$ (3.9)

Damit ergibt sich nun durch Multiplikation der erhaltenen Ungleichung mit $n$ :
$----- ----- n prod -1 n sum -1 n prod -1 n n- V~ 1 ai < ai + n-1 V~ ai i=1 i=1 i=1$
Wir bringen den einen Term auf die linke Seite:
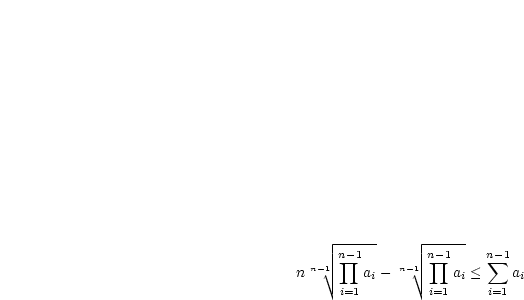
$----- ----- n prod -1 n- prod 1 n sum -1 n n- V~ 1 ai - n- V~ 1 ai < ai i=1 i=1 i=1$

$n--1-- n-1 (n - 1) n- V~ 1 prod a < sum a i=1 i i=1 i$
Division durch $n - 1$ ergibt dann schließlich unsere zu beweisende Aussage $A(n - 1)$ :
$|----------------------| | n prod -1 1 n sum -1 | |n-1 V~ ai <----- ai | -----i=1-----n---1i=1---|$

Übung:

Zeigen Sie mit vollständiger Induktion:

n sum (-1)k+1k2 = (- 1)n+1 n(n-+-1) k=1 2

3.7.3 Definition durch Induktion/Rekursive Definition

D(n) sei Gr¨oße, die von n (- N abh¨angt. D(n) soll f¨ur alle n definiert werden.

Man definiere $D(1)$ .
$D(k)$ sei für $k (- N$ beliebig und schon definiert.
Dann definiere man hiermit $D(k +1)$ .

Beispiele:

Die Fakultät:
Man definiere $1! := 1$ . Dann folgt daraus:
$|------------------| (k-+1)! :=-(k-+-1).k!$
Damit berechnet sich also die Fakultät folgendermaßen:
$n! = 1 .2.3.4 .5.....n$
Das Summenzeichen:
Man definiere $sum 1 aj := a1 j=1$ . Damit haben wir:
$|----------------------| k+1 ( k ) | sum aj := sum aj + ak+1| j=1 j=1 | ------------------------$
Potenzen:
Man definiere $a1 := a$ . Dann resultiert:
$|-------------| |ak+1 := (ak).a ---------------$

M1 = {x|x > 0},M2 = {x|- 1 < x < 0}

Es seien x1,...,xn (- M1 (oder (- M2)

Satz:

$n prod (1+ xn) > 1 +x1 + x2 + ...+ xn j=1$ für $n (- N$

Beweis:

Induktionsanfang: $1 +x1 links 1 + x1 rechts (w)$
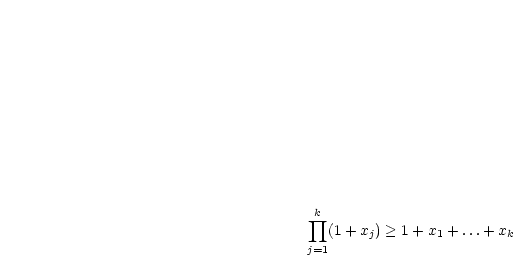
Induktionsschluß: $k prod (1+ xj) > 1 + x1 + ...+ xk j=1$
- Induktionsvoraussetzung:
  Es gelte für $j > 1$ :
  $k k prod (1+ xj) > 1 + sum xj j=1 j=1$
- Induktionsbehauptung: $k+ prod 1 k sum +1 (1+ xj) > 1 + xj j=1 j=1$
$( ) ( ) k+ prod 1 prod k sum k k sum +1 sum k k sum +1 (1+xj) = (1+ x0) (1-+-xk+1)> 1+ xj (1+-xk+1)= 1+ xj+xk+1 xj > 1+ xj j=1 j=1 >0 j=1 >0 j=1 ---j=1- j=1 >0$

3.7.4 BERNOULLIsche Ungleichung

Satz:

Für $x > - 1$ und $n (- N$ gilt:

$(1+ x)n > 1+ nx$

Beweis:

Wir benutzen oben bewiesene Ungleichung:

prod n (1 + xn) > 1 +x1 + x2 + ...+ xn f¨ur n (- N j=1

Setze nun $x1 = x2 = ...= xn = x$ . Damit folgt:

n prod (1+ x) = (1 + x)n > 1+ nx j=1

Damit ist die BERNOULLIsche Ungleichung bewiesen.

3.7.5 Geometrische Summe

$q /= 1$ . Dann gilt für jedes $n (- N U {0}$ :

sum n n-1 1 + q+ q2 + ...+qn = qk = 1--q---- k=0 1- q

Setze:

sum n S = qk = 1 + q+ q2 + ...+ qn } n+1 k=0 S - qS = 1- q = S(1- q) qS = = q + q2 + ...+ qn + qn+1

Übung:

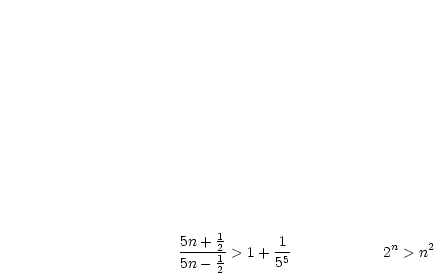
Für welche $n (- N$ gilt: $5n+ 1 1 -----21> 1 + -5 2n > n2 5n- 2 5$
Dies gilt nur für $1 < n < 625$

Satz:

$n$ verschiedene Elemente $a 1$ , $a 2$ , $...$ , $a n$ lassen sich auf $n!$ verschiedene Arten anordnen.

Induktionsanfang:
Nach der Formel gibt es $P1 = 1! = 1$ Möglichkeiten, um ein einziges Element anzuordnen. Dies ist wohl war.
Induktionsschluß:
- Induktionsvoraussetzung:
  Für ein $n > 1$ gelte $P = n! n$ .
- Induktionsbehauptung: $Pn+1 = (n + 1)!$
$a .a .....a 1 2 n+1$
Betrachte alle Anordnungen, bei denen $ak$ am Anfang steht: $n!$ . Wegen $k = 1$ , $2$ , $...$ , $n + 1$ erhält man insgesamt $(n+ 1)n! = (n +1)!$ .

3.7.6 Binomialkoeffizient

a (- R,k (- N

(a) a.(a -1) .(a - 2).....(a - k+ 1) (a ) k = --------------k!--------------, 0 = 1

Übung:

( ) ( ) ( ) a + a = a + 1 k k+ 1 k + 1

Es sei speziell $a = n (- N$ . Dann gelten:

( ) n = 0 k > n k

( ) 3 = 3-.2.1.0-.(--1)= 0 5 5!

Für $k < n$ gilt:

(n-k)! ( ) ------------ ------------ ( ) n = n-.(n--1).(n---2)-.(n---k+-1)(n--k)-.(n---k--1).....3.2-.1 = ----n!---= n k k!.(n - k)! k!(n- k)! n- k

Satz (Lotto/Kombinationen):

Es seien $k$ , $n (- N$ , $k (- n$ . Die Anzahl $Kk n$ der $k$ -elementigen Teilmengen einer $n$ -elementigen Menge ist $(n) k$ .

Beweis mit Vollständiger Induktion:

Induktionsanfang: $(1 ) n = 1(==> k = 1) Kkn = 1 = 1 (wahr)$
Induktionsschluß:
- Induktionsvoraussetzung: $(n) Kkn = f¨ur 1 < k < n und n,k (- N k$
- Induktionsbehauptung: $( ) k n + 1 Kn+1 = k f¨ur 1 < k < n+ 1$
Induktionsbeweis:
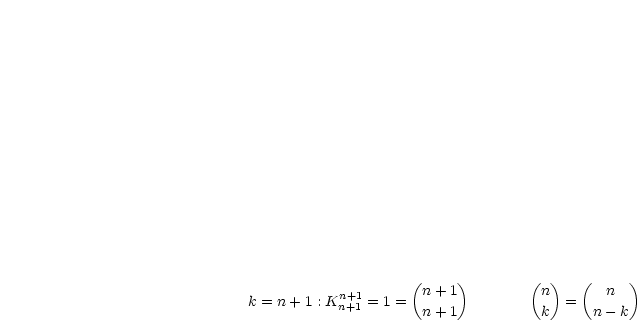
- 1.Fall: $n+1 (n + 1) (n ) ( n ) k = n+ 1 : Kn+1 = 1 = n+ 1 k = n - k$
- 2.Fall: $(n + 1) k < n : Kkn+1 = k$
Teile alle Teilmengen in zwei Klassen $T 1$ , $T 2$ wie folgt:
- In $T1$ liegen alle $k$ -elementigen Teilmengen, zu denen $an+1$ gehört. $( ) n k -1$
- In $T2$ liegen alle $k$ -elementigen Teilmengen, die $an+1$ nicht enthalten. $( ) n k$

[next] [prev] [prev-tail] [front] [up]